Rigid Wall

There are four types of rigid walls available in Radioss:

Infinite Plane
Infinite Cylinder with Diameter D
Sphere with Diameter D
Parallelogram

Each wall can be fixed or moving.

A kinematic condition is applied on each impacted secondary node. Therefore, a secondary node cannot have another kinematic condition; unless these conditions are applied in orthogonal directions.

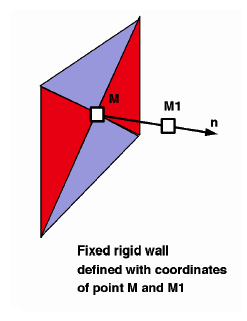
Fixed Rigid Wall

A fixed wall is a pure kinematic option on all impacted secondary nodes. It is defined using two points, M and M1. These define the normal, as shown in Figure 1.

Moving Rigid Wall

A moving rigid wall is defined by a node number, N, and a point, M1. This allows a normal to be calculated, as shown in Figure 2.

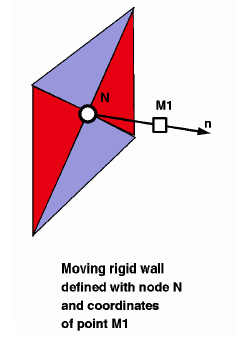
The motion of node N can be specified with fixed velocity, or with an initial velocity. For simplification, an initial velocity and a mass may be given at the wall definition level.

A moving wall is a main secondary option. Main node defines the wall position at each time step and imposes velocity on impacted secondary nodes. Impacted secondary node forces are applied to the main node. The secondary node forces are computed with momentum conservation. The mass of the secondary nodes is not transmitted to the main node, assuming a large rigid wall mass compared to the impacted secondary node mass.

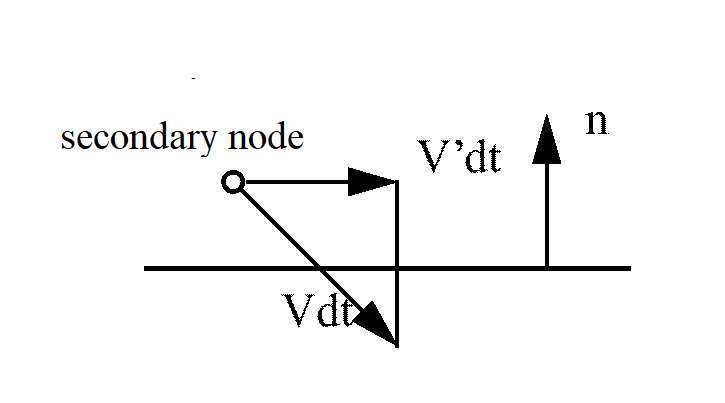
Secondary Node Penetration

Secondary node penetration must be checked. Figure 3 shows how penetration is checked.

If penetration occurs, a new velocity must be computed. This new velocity is computed using one of three possible situations.

Sliding
Sliding with Friction
Tied

For a node which is allowed to slide along the face of the rigid wall, the new velocity ${\overset{⇀}{V}}^{'}$ is given by:

{\overset{⇀}{V}}^{'} = \vec{V} - (\vec{V} \cdot \vec{n}) \vec{n}

A friction coefficient can be applied between a sliding node and the rigid wall. The friction models are developed in Interface Friction.

For a node that is defined as tied, once the secondary node contacts the rigid wall, its velocity is the same as that of the wall. The node and the wall are tied. Therefore:

{\overset{⇀}{V}}^{'} = 0

Rigid Wall Impact Force

The force exerted by nodes impacting onto a rigid wall is found by calculating the impulse by:

\overset{⇀}{I} = \sum_{i = I}^{N} {\vec{F}}_{i} Δ t = \sum_{i = I}^{N} Δ m_{i} ({\vec{V}}_{i} - \vec{W})

Where,

$N$: Number of penetrated secondary nodes
$\vec{W}$: Wall velocity

The force can then be calculated by the rate of change in the impulse:

\vec{F} = \frac{d \vec{I}}{d t}