Rigid Body

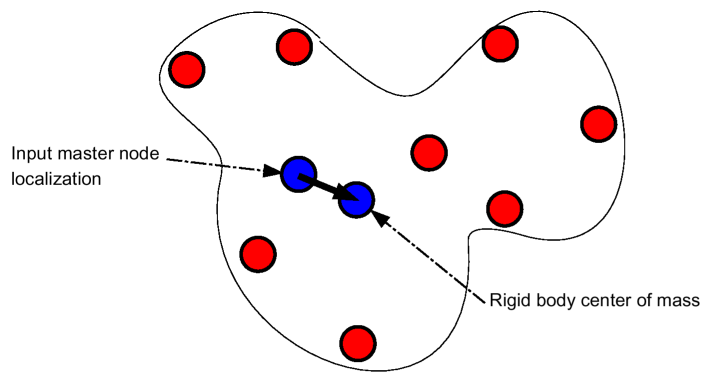
A rigid body is defined by a main node and its associated secondary nodes. Mass and inertia may be added to the initial main node location. The main node is then moved to the center of mass, taking into account the main node and all secondary node masses. Figure 1 shows an idealized rigid body.

Rigid Body Mass

The mass of the rigid body is calculated by:

m = m^{M} + \sum_{I} m^{I}

The rigid body's center of mass is defined by:

x^{G} = \frac{m^{M} x^{M} + \sum m^{I} x^{I}}{m}

y^{G} = \frac{m^{M} y^{M} + \sum m^{I} y^{I}}{m}

z^{G} = \frac{m^{M} z^{M} + \sum m^{I} z^{I}}{m}

Where,

$m^{M}$: Main node mass
$m^{I}$: Secondary node masses
$x^{G}$ , $y^{G}$ , $z^{G}$: Coordinates of the mass center

Rigid Body Inertia

The six components of inertia of a rigid body are computed by:

I_{x x} = J_{x x}^{M} + m^{M} ({(y_{M} - y_{G})}^{2} + {(z_{M} - z_{G})}^{2}) + \sum_{i} (I_{x x}^{i} + m^{i} ({(y_{i} - y_{G})}^{2} + {(z_{i} - z_{G})}^{^{2}}))

I_{y y} = J_{y y}^{M} + m^{M} ({(x_{M} - x_{G})}^{2} + {(z_{M} - z_{G})}^{2}) + \sum_{i} (I_{y y}^{i} + m^{i} ({(x_{i} - x_{G})}^{2} + {(z_{i} - z_{G})}^{^{2}}))

I_{z z} = J_{z z}^{M} + m^{M} ({(x_{M} - x_{G})}^{2} + {(y_{M} - y_{G})}^{2}) + \sum_{i} (I_{z z}^{i} + m^{i} ({(x_{i} - x_{G})}^{2} + {(y_{i} - y_{G})}^{^{2}}))

I_{x y} = J_{x y}^{M} + m^{M} ({(x_{M} - x_{G})}^{} + {(y_{M} - y_{G})}^{}) + \sum_{i} (I_{x y}^{i} - m^{i} ({(x_{i} - x_{G})}^{} + {(y_{i} - y_{G})}^{^{}}))

I_{y z} = J_{y z}^{M} + m^{M} ({(y_{M} - y_{G})}^{} + {(z_{M} - z_{G})}^{}) + \sum_{i} (I_{y z}^{i} - m^{i} ({(y_{i} - y_{G})}^{} + {(z_{i} - z_{G})}^{^{}}))

I_{x z} = J_{x z}^{M} + m^{M} ({(x_{M} - x_{G})}^{} + {(z_{M} - z_{G})}^{}) + \sum_{i} (I_{x z}^{i} - m^{i} ({(x_{i} - x_{G})}^{} + {(z_{i} - z_{G})}^{^{}}))

Where,

$I_{i j}$: Moment of rotational inertia in the $i j$ direction
$J_{i j}^{M}$: Main node added inertia

Rigid Body Force And Moment Computation

The forces and moments acting on the rigid body are calculated by:

\vec{F} = {\vec{F}}^{M} + \sum_{i} {\vec{F}}^{i}

\vec{M} = {\vec{M}}^{M} + \sum_{i} {\vec{M}}^{i} + \sum_{i} S_{i} \vec{G} \times {\vec{F}}^{i}

Where,

${\vec{F}}^{M}$: Force vector at the main node
${\vec{F}}^{i}$: Force vector at the secondary nodes
${\vec{M}}^{M}$: Moment vector at the main node
${\vec{M}}^{i}$: Moment vector at the secondary nodes
$\vec{G}$: Vector from secondary node to the center of mass

Resolving these into orthogonal components, the linear and rotational acceleration may be computed as:

Linear Acceleration

γ_{i} = \frac{F_{i}}{m}

Rotational Acceleration

I_{1} α_{1} = M_{1} - (I_{3} - I_{2}) ω_{2} ω_{3}

I_{2} α_{2} = M_{2} - (I_{1} - I_{3}) ω_{1} ω_{3}

I_{3} α_{3} = M_{3} - (I_{2} - I_{1}) ω_{1} ω_{2}

Where,

$I_{i}$: Principal moments of inertia of the rigid body
$α_{1}$: Rotational accelerations in the principal inertia frame (reference frame)
$ω_{i}$: Rotational velocity in the principal inertia frame (reference frame)
$M_{i}$: Moments in the principal inertia frame (reference frame)

Time Integration

Time integration is performed to find velocities of the rigid body at the main node:

\vec{ν} (t + \frac{Δ t}{2}) = \vec{ν} (t - \frac{Δ t}{2}) + \vec{γ} (t) Δ t

\vec{ω} (t + \frac{Δ t}{2}) = \vec{ω} (t - \frac{Δ t}{2}) + \vec{α} (t) Δ t

Where, $\vec{v}$ is the linear velocity vector. Rotational velocities are computed in the local reference frame.

The velocities of secondary nodes are computed by:

{\vec{ν}}^{i} = {\vec{ν}}^{M} + S_{i} \vec{G} x \vec{ω}

{\overset{⇀}{ω}}^{i} = {\vec{ω}}^{M}

Boundary Conditions

The boundary conditions given to secondary nodes are ignored. The rigid body has the boundary conditions given to the main node only.

A kinematic condition is applied on each secondary node, for all directions. A secondary node is not allowed to have any other kinematic conditions.

No kinematic condition is applied on the main node. However, the rotational velocities are computed in a local reference frame. This reference frame is not compatible with all options imposing rotation such as imposed velocity, rotational, rigid link.

The only exception concerns the rotational boundary conditions for which a special treatment is carried out. Connecting shell, beam or spring with rotation stiffness to the main node, is not yet allowed either.