/MAT/LAW28 (HONEYCOMB)
Block Format Keyword This law describes a three dimensional nonlinear elasto-plastic material, usually used to model honeycomb or foam material.
Nonlinear elasto-plastic behavior can be specified for each orthotropic direction and shear as function of strain or volumetric strain. All degrees of freedom are uncoupled and the material is fully compressible. Tension and shear strain based failure criteria can be specified.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW28/mat_ID/unit_ID or /MAT/HONEYCOMB/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E11 | E22 | E33 | |||||||
| G12 | G23 | G31 | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_ID11 | fct_ID22 | fct_ID33 | Iflag1 | Fscale11 | Fscale22 | Fscale33 | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_ID12 | fct_ID23 | fct_ID31 | Iflag2 | Fscale12 | Fscale23 | Fscale31 | |||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| mat_title | Material title (Character, maximum 100 characters) |
|
| Initial material
density (Real) |
||
| E11 | Young's modulus in orthotropic dimension
1 (Real) |
|
| E22 | Young's modulus in orthotropic dimension
2 (Real) |
|
| E33 | Young's modulus in orthotropic dimension
3 (Real) |
|
| G12 | Shear modulus in direction
12 (Real) |
|
| G23 | Shear modulus in direction
23 (Real) |
|
| G31 | Shear modulus in direction
31 (Real) |
|
| fct_ID11 | Yield stress function identifier in
direction 11 (Integer) |
|
| fct_ID22 | Yield stress function identifier in
direction 22 (Integer) |
|
| fct_ID33 | Yield stress function identifier in
direction 33 (Integer) |
|
| Iflag1 | Strain formulation for yield functions
11, 22, and 33. 6
(Integer) |
|
| Fscale11 | Scale factor for yield stress function
in direction 11. Default = 1.0 (Real) |
|
| Fscale22 | Scale factor for yield stress function
in direction 22. Default = 1.0 (Real) |
|
| Fscale33 | Scale factor for yield stress function
in direction 33. Default = 1.0 (Real) |
|
| Failure strain in tension in direction
11. (Real) |
||
| Failure strain in tension in direction
22. (Real) |
||
| Failure strain in tension in direction
33. (Real) |
||
| fct_ID12 | Shear yield stress function identifier
in direction 12. (Integer) |
|
| fct_ID23 | Shear yield stress function identifier
in direction 23. (Integer) |
|
| fct_ID31 | Shear yield stress function identifier
in direction 31. (Integer) |
|
| Iflag2 | Strain formulation for shear yield
functions 12, 23, and 31.
(Integer) |
|
| Fscale12 | Scale factor for shear yield function
12. Default = 1.0 (Real) |
|
| Fscale23 | Scale factor for shear yield function
23. Default = 1.0 (Real) |
|
| Fscale31 | Scale factor for shear yield function
31. Default = 1.0 (Real) |
|
| Failure strain in shear direction
12. (Real) |
||
| Failure strain in shear direction
23. (Real) |
||
| Failure strain in shear direction
31. (Real) |
Example (Steel)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HONEYCOMB/1/1
Steel
# RHO_I
7.8E-9
# E_11 E_22 E_33
200000 200000 200000
# G_12 G_23 G_31
100000 100000 100000
# fct_ID11 fct_ID22 fct_ID33 Iflag1 Fscale11 Fscale22 Fscale33
1 1 1 0 0 0 0
# Eps_max11 Eps_max22 Eps_max33
0 0 0
# fct_ID12 fct_ID23 fct_ID31 Iflag2 Fscale12 Fscale23 Fscale31
2 2 2 0 0 0 0
# Eps_max12 Eps_max23 Eps_max31
0 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
FUNCTION: 1
# X Y
0 200
.5 200
1.5 200000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
FUNCTION: 2
# X Y
0 100
.5 100
1.5 100000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
Comments
- This material law requires solid orthotropic property /PROP/TYPE6 (SOL_ORTH). Material is compatible with hexa and tetra elements, including 10-node tetrahedron elements. Refer to Material Compatibility for more compatibility information.
- Material orthotropic coordinate
system for each element (directions 1, 2, and 3) are specified in the property card
/PROP/TYPE6 either through a given skew system or related to element
coordinate system.
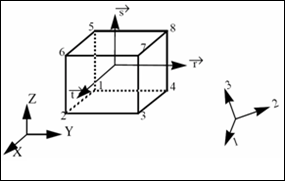
Figure 1. - All element degrees
of freedom are fully uncoupled.
Elastic case example:
- For each tension/compression and shear direction, the true stress as function of a
true volumetric strain
, or a true strain
can be specified.Sign conventions for strain are:
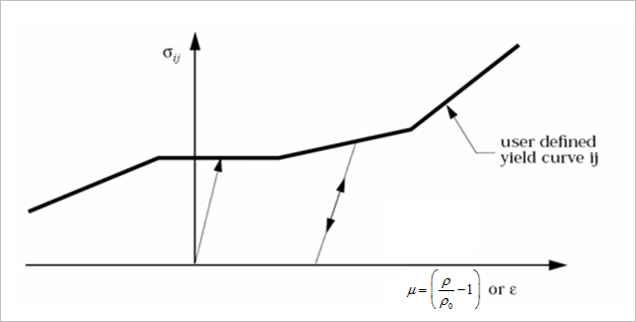
Figure 2.The stress values should always be positive. The following sign conventions for strain are used:Strain Definition Compression Tension Volumetric strain (Iflag1 =0) + - Strain (Iflag1 =1) - + Strain (Iflag1 =-1) + - - For large strain formulations defined
in the property using Ismstr > 1:
(1) For small strains defined in the property using Ismstr = 1:(2) Where, is the initial length.
- When switching from a volumetric strain formulation to a strain formulation, Iflag1 = -1 or Iflag2 = -1 allows the same function definition to be retained.
- If one of the tension strain or shear strain failures is reached, the element is deleted.