OS-V: 0080 Buckling of Shells and Composites with Offset

A test of influence of offset on buckling solution for shells, including composite with offset Z0 and element offset ZOFFS.

Model Files

Before you begin, copy the file(s) used in this problem to your working directory.

Benchmark Model

Here, you solve several problems to calculate the critical load on different conditions. The model is a simply supported beam of height 1 mm, breadth 2 mm and length 100 mm with one end constrained in all DOFs and an axial load applied on the other end.

The material properties for the beam are:

MAT1
Young's Modulus: 1 x 10⁶ N/mm²
Poisson's Ratio: 0.0
Density: 2 kg/mm³
Thermal Expansion Coefficient: 1 x 10^-4 ºC^-1
Reference Temperature for Thermal Loading: 300ºC

The different case description of the problem are:

Buckling without offset.
Buckling with moment equivalent to offset.
Buckling with offset created by a frame.
Buckling with offset applied through ZOFFS.
Buckling of composite with non-symmetrical layup.
Buckling of composite with offset.

The theoretical critical buckling load is calculated using the Euler Buckling equation:(1)

f_{c r i t} = π \frac{E I}{{(K L)}^{2}}

Where,

$f_{c r i t}$: Maximum or critical force
$E$: Modulus of elasticity
$I$: Area moment of inertia (second moment of area)
$L$: Unsupported length of the beam
$K$: Column effective length factor (for one end fixed and the other end free, $K$ =2)

Results

Quantity	Theoretical	No-offset	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1208	0.997937
$λ$ _cr⁽²⁾	16.449	16.513	0.996124
$λ$ _cr⁽³⁾	37.011	37.701	0.981698
$λ$ _cr⁽⁴⁾	102.81	108.19	0.950273

Quantity	Theoretical	No-offset + Moment	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1208	0.997937
$λ$ _cr⁽²⁾	16.449	16.513	0.996124
$λ$ _cr⁽³⁾	37.011	37.701	0.981698
$λ$ _cr⁽⁴⁾	102.81	108.19	0.950273

Quantity	Theoretical	C-Frame	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1208	0.997937
$λ$ _cr⁽²⁾	16.449	16.513	0.996124
$λ$ _cr⁽³⁾	37.011	37.700	0.981724
$λ$ _cr⁽⁴⁾	102.81	108.19	0.950273

Quantity	Theoretical	ZOFFS	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1208	0.997937
$λ$ _cr⁽²⁾	16.449	16.513	0.996124
$λ$ _cr⁽³⁾	37.011	37.700	0.981724
$λ$ _cr⁽⁴⁾	102.81	108.19	0.950273

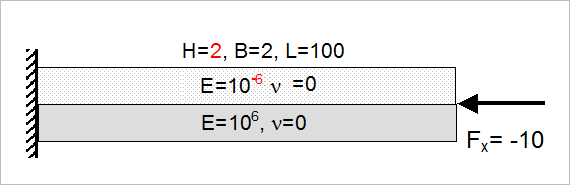
Quantity	Theoretical	Non-symmetric Layup	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1203	0.998058
$λ$ _cr⁽²⁾	16.449	16.510	0.996305
$λ$ _cr⁽³⁾	37.011	37.663	0.982689
$λ$ _cr⁽⁴⁾	102.81	107.89	0.952915

Quantity	Theoretical	Offset Composite	Normalized
$λ$ _cr⁽¹⁾	4.1123	4.1203	0.998058
$λ$ _cr⁽²⁾	16.449	16.510	0.996305
$λ$ _cr⁽³⁾	37.011	37.663	0.982689
$λ$ _cr⁽⁴⁾	102.81	107.89	0.952915