Glossary
- Term
- Definition
- Conjugate Gradient
- An iterative algorithm for the numerical solution of symmetric and positive-definite systems of linear equations. A key feature of this algorithm is that the direction at step K is conjugate (A-orthogonal) to the directions at all the previous steps.
- Constrained Optimization
- Constrained optimization is the process of optimizing (usually minimizing) an objective function with respect to some design variables in the presence of constraints on those designs variables. These constraints can be bounds on the design space, equality constraints and inequality constraints. The sought after solution is required to satisfy all the constraints.
- Constraints
- Constraints are algebraic relationships amongst the design variables that a
solution for the optimization must satisfy. The algebraic relationships come
in 3 flavors:
- Simple bound constraints
- Equality or bilateral constraints
- Inequality or unilateral constraints
- Cost Function
- Often called the objective function, this is the quantity that is to be minimized in an optimization process.
- Design Bound Constraints
- These specify lower bounds (bL) and upper bounds (bLon the design parameters that the solution is required to satisfy. Thus at any feasible design point b*, bL≤ b* ≤ bU
- Design Variables
- These are the quantities that are to be determined in the optimization problem. In the CAE context, design variables are used to define parametric models. By changing the values for design variables in a model, you can change the model. An optimizer will change the values of the design variables for a model in its quest to find an optimum solution.
- Equality Constraints
- A set of nonlinear or linear algebraic equations that the solution must satisfy. The equality relationships are usually expressed in the form
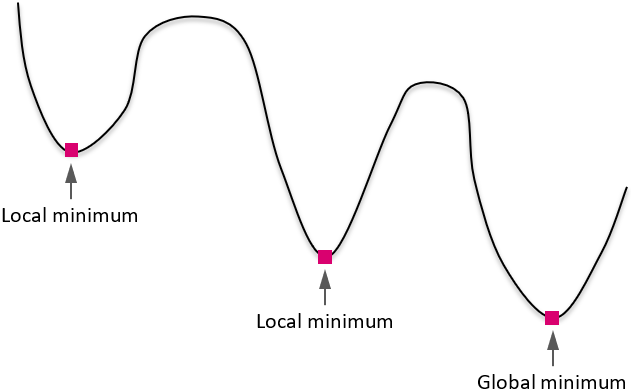
- Global Optimization
- An optimization process wherein the global minimum of a function is sought.
Let f() be the function being minimized, and b the design variables. A
solution b* is said to be a global minimum if f (b*) ≤
f (b) for all b ≠ b*.
- Gradient
- If f(x1, ..., xn) is a differentiable, real-valued
function of several variables, its gradient is the vector whose components
are the n partial derivatives of f.
- Hessian Matrix
- The Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him.
- Jacobian Matrix
- The Jacobian matrix is the matrix of all first-order partial derivatives of
a function f. It is named after the mathematician Carl Gustav Jacob Jacobi
(1804–1851).
- Line Search
- In optimization, the line search strategy is one of two basic iterative approaches to find a local minimum x* of an objective function f.
- Local Optimization
- An optimization process wherein the local minimum of a function is sought.
Let f() be the function being minimized, and b the design variables. Let
b0 be an initial guess for b. A solution b* is
said to be a local minimum if f’(b*) = 0 and f’’(b*)
< 0.

- Multi-Objective Optimization
- An optimization problem in which the objective is not a single scalar function f but a set of scalar functions [f1, f2, …fN] that is to be optimized. Often, the objectives are conflicting.
- Objective Function
- Often called the cost function, this is the quantity that is to be minimized in an optimization process.
- Design Optimization
- The selection of the values of the best design variables given a design space, a cost function and, optionally, some constraints on the design variables.
- Pareto Optimal Solution
- Often in multi-objective optimization there are conflicting objectives, such
as cost and performance. The answer to a multi-objective problem is usually
not a single point. Rather, it is a set of points called the Pareto front.
Each point on the Pareto front satisfies the Pareto optimality criterion, which is stated as follows: a feasible vector X* is Pareto optimal if there exists no other feasible solution X which would improve some objective without causing a simultaneous worsening in at least one other objective.
A feasible point X that CAN be improved on one or more objectives simultaneously without worsening any of the others is not Pareto optimal.
- Response Variable
- Model behavior metrics are captured in terms of Response Variables. The optimizer in MotionSolve works with Response Variables.
- Search Method
- A search method is a mathematical algorithm used by the optimizer in MotionSolve to reduce the cost function. The optimizer in MotionSolve supports many different search methods. These are: L-BFGS-B, TNC, COBYLA, SLSQP, dogleg, trust-ncg, Nelder-Mead, Powell, CG, BFGS and Newton-CG.
- State Variable
- A state variable is one of the set of variables that are used to describe the mathematical "state" of a dynamical system.
- Steepest Descent
- Steepest descent is a first-order iterative optimization algorithm. To find a local minimum of a function using steepest descent, take steps proportional to the negative of the gradient (or of the approximate gradient) of the function at the current point.
- Unconstrained Optimization
- An unconstrained problem has no constraints. Thus there are no equality or inequality constraints that the solution b, has to satisfy. Furthermore there are no design limits either.