System Reliability Optimization (SRO)

Searches for designs that satisfy design requirements with a required probability of success for the system as a whole.

When there are multiple reliability constraints, it becomes important to account for the system reliability as a whole, rather than the reliability of individual constraints.

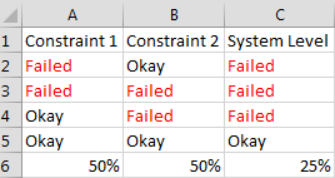
As an example, consider a design with two probabilistic constraints that are each individually 50% reliable. In Figure 1, the system is 25% reliable since the four runs do not include failures.

Usability Characteristics

The reliability assessments are not based on a Most Probable Point (MPP) formulation, but instead is based on Monte Carlo simulations using advanced response surface techniques.
System Reliability Optimization requires fewer runs than MPP optimizers, such as Sequential Optimization and Reliability Assessment, ARSM-Based Sequential Optimization and Reliability Assessment , and Single Loop Approach.
Consists of a global search capability.
Terminates when there are not enough remaining evaluations to complete the next iteration.
Supports input variable constraints.
All defined constraints are part of the system level constraint. The reliability of an individual constraint will be imposed when the constraint is defined as random. If the constraint is deterministic, it is only considered at the system level.
For robust optimizations, the optimization problem is formulated as a multi-objective problem between the nominal objective goal and minimizing the objective's standard deviation. This results presents a family of optimal designs that explore the trade-off between performance and robustness. Use the Optima tab to visualize the trade-off.
Supports input variable constraints.
The size of the first iteration is controlled by the sum of the Initial Sampling Points and Local Sampling Points settings. The number of evaluations in subsequent iterations is controlled by sum of the Local Sampling Points and Global Sampling Points settings. All the designs generated in one iteration can be executed in parallel.

Settings

In the Specifications step, change method settings from the Settings and More tabs.

Table 1. Settings Tab
Parameter	Default	Range	Description
Number of Evaluations	200	> 0 Integer	Maximum number of iterations allowed.
System Reliability (%)	0.98	Numeric > 0 < 100	Defines the system level reliability constraint.
Robust Optimization	No	No or Yes	Defines whether this is a robust optimization or not. No Do not use robust optimization. Yes Use robust optimization.
System Reliability Tol.	0.1	> =0	The allowable percentage violation on system reliability. The design is acceptable if system reliability is not less than System Reliability (%) minus this value.
On Failed Evaluation	Terminate optimization	Terminate optimization Ignore failed evaluations	Determines how to react to evaluation failures.

Table 2. More Tab
Parameter	Default	Range	Description
Max Failed Evaluations	20000	Integer > 0	When On Failed Evaluations is set to Ignore failed evaluations (1), the optimizer will tolerate failures until this threshold for Max Failed Evaluations. This option is intended to allow the optimizer to stop after an excessive amount of failures.
Initial Sampling Points	50	Integer > 0	Number of initial sample points. Tip: Recommended range: 20 - 100
Global Sampling Points	2	Integer > 0	Number of samples required per iteration spread throughout the design space. Used to estimate global effects, and avoid a local minima. Tip: Recommended: 1-10
Local Sampling Points	5	Integer > 0	Number of samples required per iteration localized around current iterate. Used to build an accurate response surface in the vicinity of the iterate. Tip: Recommended: 3-10
Monte Carlo Points	1000	Integer > 0	Number of internal Monte Carlo runs used to calculate the reliability. Tip: Recommended: 500-10000
Random Seed	1	Integer 0 to 10000	Controlling repeatability of runs depending on the way the sequence of random numbers is generated. 0 Random (non-repeatable). >0 Triggers a new sequence of pseudo-random numbers, repeatable if the same number is specified.
Stop after no Improvement	1000	Integer > 0	Terminate the optimization if the number of iterations without improvement exceeds this value.
Use Inclusion Matrix	With Initial	With Initial Without Initial	With Initial Runs the initial point. The inclusion set and initial point are used to build the initial response surface. Without Initial Does not run the initial point. The inclusion set is used to build the initial response surface.