Sequential Optimization and Reliability Assessment (SORA)

A reliability-based design optimization method. Reliability-based design optimization (RBDO) methods take uncertainties in the design into account and search for designs that satisfy the design requirements with a required probability of success.

A reliability-based design problem is formulated as:

Objective: min f(x, r, p)
Constraints: P(g(x, r, p ≤ 0.0) > PS

where,

x: Deterministic input variables
r: Random input variables (affect the design but are subject to uncertainties)
p: Pure random parameters (variables we have no control over but affect the design, such as humidity and temperature)

Usability Characteristics

An extension of Sequential Optimization and Reliability Assessment is implemented in HyperStudy to allow for robust design optimization. Robust design optimization attempts to minimize the objective variance in order to reduce its sensitivity to design variations and consequently increase the design's robustness. The implementation in HyperStudy is based on the use of percentiles for the objective function and is turned on via the Robust Optimization setting in the Specification step.
Sequential Optimization and Reliability Assessment is the most accurate of the three RBDO methods available in HyperStudy. It is also the most expensive.
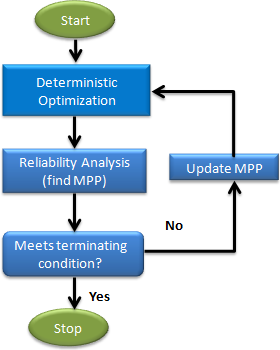
Sequential Optimization and Reliability Assessment terminates if one of the conditions below are met:
- One of the two convergence criterias are met.
  - The absolute objective change is less than a convergence tolerance value (Termination Criteria) and there is no constraint violation (Constraint Violation Tol. (%)).
  - The relative objective change is less than a convergence tolerance value (Termination Criteria) and there is no constraint violation (Constraint Violation Tol. (%)) in the last design.
- The maximum number of allowable iterations (Maximum Iterations) is reached.
An exception is when the current objective is worse than the previous objective and the constraint violation of the previous design is within allowable violation. When this occurs, Sequential Optimization and Reliability Assessment will be terminated.
The reliability analysis is carried out by searching for the most probable point (MPP). Issues such as non-uniqueness of the MPP and highly non-linear output response functions can reduce the accuracy of the reliability calculation.
The number of evaluations in each iteration is automatically set and varies due to the finite difference calculations used in the sensitivity calculation. The number of evaluations in each iteration is dependent of the number of variables. The evaluations required for the finite difference are executed in parallel. The evaluations required for the line search are executed sequentially.

Figure 1. Sequential Optimization and Reliability Assessment Process Phases

Settings

In the Specifications step, change method settings from the Settings and More tabs.

Note: For most applications the default settings work optimally, and you may only need to change the Maximum Iterations and Robust Optimization.

Table 1. Settings Tab
Parameter	Default	Range	Description
Maximum Iterations	25	> 0	Maximum number of iterations allowed.
Robust Optimization	No	No or Yes	Defines whether this is a robust optimization or not. No Do not use robust optimization. Yes Use robust optimization.
Robust Min %	95.0	> 50 < 100	Defines the percentile value of robust optimization for minimization objective.
Robust Max %	5.0	> 0 < 50	Defines the percentile value of robust optimization for maximization objective.
On Failed Evaluation	Terminate optimization	Terminate optimization Ignore failed evaluations	Terminate optimization Terminates with an error message when an analysis run fails. Ignore failed evaluations Ignores the failed analysis run.

Table 2. More Tab
Parameter	Default	Range	Description
Angle Convergence Tol.	0.25	> 0.0	Angle convergence tolerance for inverse MPP search, in unit of degrees. If the angle between the vector of $\bar{u}$ (design point in standard normal distribution space) and the negative gradient falls within the tolerance, then inverse MPP search is regarded as converged. Tip: A smaller value favors a higher precision of reliability analysis, but more computational effort is needed.
Termination Criteria	1.0e-4	> 0.0	Termination tolerance. If the absolute or relative change of the objective value is less than this value, and the constraint violation is not larger than this value, then Sequential Optimization and Reliability Assessment will be terminated. There also must not be any constraint with an allowable violation that has been exceeded in the last design. ${\begin{cases} c_{\max}^{k} \leq g_{\max} \\ i f \| f^{k} - f^{k - 1} \| < Termination Criteria \\ o r \frac{\| f^{k} - f^{k - 1} \|}{\| f^{k - 1} \| + 10^{- 10}} < Termination Criteria \end{cases}$ Where, $f$ is the objective; $k$ is the current iteration number; $c_{\max}$ is the maximum constraint violation; $g_{\max}$ is the allowable constraint violation; Termination Criteria is the value of the termination criteria. An exception is when the current objective is worse than the previous objective and the constraint violation of the previous design is within allowable violation, Sequential Optimization and Reliability Assessment will be terminated. ${\begin{cases} c_{\max}^{k - 1} \leq g_{\max} \\ {\begin{cases} f^{k} > f^{k - 1}, minimization \\ f^{k} < f^{k - 1}, maximization \end{cases} \end{cases}$