Adaptive Response Surface Method (ARSM)

Internally builds response surfaces and adaptively updates them as new evaluations are available.

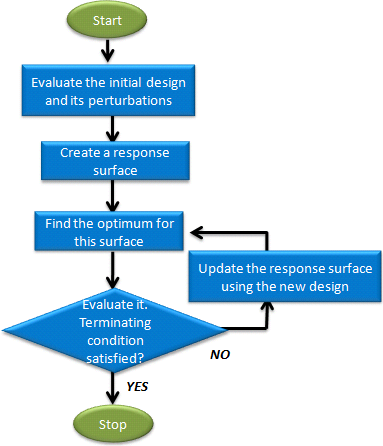
The first response surface the Adaptive Response Surface Method builds is a linear regression polynomial, then it finds the optimum on this surface and validates it with the exact simulation. If the output response values from the response surface and the exact simulation are not close; the Adaptive Response Surface Method updates the surface with the new evaluation and finds the optimum in this updated surface. This loops is repeated until one of the convergence criteria is met.

Usability Characteristics

Adaptive Response Surface Method is the default method. However, if the number of input variables is large, or if a global optima is required, then it is suggested that you use Global Response Search Method instead.
For Revisions A-multi and B-multi, Adaptive Response Surface Method can take advantage of parallel execution. The number of runs in the iterative stages after N+1 evaluations (N is the number of variables) can be controlled by the setting parameter Points per iteration.
It is an efficient optimization method because it utilizes response surfaces. It is recommend to use Adaptive Response Surface Method directly on a solver and not on a Fit.
In the case of a failed run, it is possible to ignore a failed analysis or terminate an optimization. When omitting failed runs, the optimizer will back up half of a step between the failed run and the previous design.
Adaptive Response Surface Method terminates when one of the following conditions are met:
- One of the convergence criteria is satisfied.
- The maximum number of allowable analysis (Maximum Iterations) is reached.
- An analysis fails and the Terminate optimization option is the default (On Failed Evaluation).
Supports input variable constraints.
The algorithm begins with N+1 evaluations, where N is the number of design variables. When SRSM is set to Response Surface, control the number of initial evaluations using the Sample Points parameter. The number of evaluations in subsequent iterations is controlled by the Points per Iteration setting. Evaluations are created sequentially by default. Adjust the Revision setting to use muli variants to execute evaluations in parallel.

Figure 1. Adaptive Response Surface Method Process Phases

Settings

In the Specifications step, change method settings from the Settings and More tabs.

Note: For most applications the default settings work optimally, and you may only need to change the Number of Evaluations and On Failed Evaluation.

Table 1. Settings Tab
Parameter	Default	Range	Description
Number of Evaluations	25	>0	Maximum number of analyses (only for Adaptive Response Surface Method number of analysis is equal to number of iterations) allowed.
Absolute Convergence	0.001	>0.0	Determines an absolute convergence tolerance, which is constant and equal to Absolute Convergence, times the initial objective function value. The design has converged when there are two consecutive designs for which the absolute change in the objective function is less than this tolerance. There also must not be any constraint whose allowable violation is exceeded in the last design. Note: A larger value allows for faster convergence, but worse results could be achieved. ${\begin{matrix} c_{\max}^{k} \leq g_{\max} \\ f^{i} - f^{i - 1} \| < \max (ε \| f^{0} \|, 10^{- 19}) \\ i = k, k - 1 \end{matrix}$ Where $f$ is the objective value; $f^{0}$ is the objective value of the initial design; $k$ is the current iteration number; $ε$ is the absolute convergence parameter; $c_{\max}$ is the maximum constraint violation; $g_{\max}$ is the allowable constraint violation.
Relative Convergence (%)	1.0	>0.0	The design has converged if the relative (percent) change in the objective function is less than this value for two consecutive designs. There also must not be any constraint whose allowable violation is exceeded in the last design. Note: A larger value allows for faster convergence, but worse results could be achieved. ${\begin{matrix} c_{\max}^{k} \leq g_{\max} \\ \frac{\| f^{i} - f^{i - 1} \|}{\| f^{i - 1} \| + 10^{- 6}} < ε \\ i = k, k - 1 \end{matrix}$ Where, $f$ is the objective value; $k$ is the current iteration number; $ε$ is the relative convergence parameter; $c_{\max}$ is the maximum constraint violation; $g_{\max}$ is the allowable constraint violation.
Design Variable Convergence	0.001	>0.0	Input variable convergence parameter. Design has converged when there are two consecutive designs for which the change in each input variable is less than both (1) Design Variable Convergence times the difference between its bounds, and (2) Design Variable Convergence times the absolute value of its initial value (simply Design Variable Convergence if its initial value is zero). There also must not be any constraint whose allowable violation is exceeded in the last design. Note: A larger value allows for faster convergence, but worse results could be achieved. $\begin{array}{l} {\begin{matrix} \| x_{j}^{i} - x_{j}^{i - 1} \| < γ \cdot (x_{j}^{U} - x_{j}^{L}) \\ {\begin{matrix} \| x_{j}^{i} - x_{j}^{i - 1} \| < γ \cdot \| x_{j}^{0} \|, {if(x}_{j}^{0} \neq 0) \\ \| x_{j}^{i} - x_{j}^{i - 1} \| < γ, {if(x}_{j}^{0} =0) \end{matrix} \\ c_{\max}^{k} \leq g_{\max} \end{matrix} \\ i = k, k - 1; j = 1, 2, ..., n \end{array}$ Where, $x$ is input variable; $x^{0}$ is the initial design; $x^{L}$ , $x^{U}$ are lower bound and upper bound of input variables respectively; $k$ is the current iteration number; $n$ is the number of input variables; $y$ is the input variable convergence parameter.
On Failed Evaluation	Terminate optimization	Terminate optimization Ignore failed evaluations	Terminate optimization Terminates with an error message when an analysis run fails. Ignore failed evaluations Ignores the failed analysis run, reduces the preceding step size by 50%, and attempts the analysis again.

Table 2. More Tab
Parameter	Default	Range	Description
Initial Linear Move	By DV Initial	By DV Initial By DV Bounds	By DV initial Initial move = Initial Input Perturbation * Move Limit Fraction * abs(INI). Default when initial value of input variable is non-zero. An exception is that initial move will be set to minimum move if it is less than minimum move. Minimum move = Minimal Move Factor * (UB-LB) if (UB-LB) is less than 1. Minimum move = Minimal Move Factor if (UB-LB) is not less than 1 and absolute value of INI is less than 1. Minimum move = Minimal Move Factor * min((UB-LB),abs(INI)) if (UB-LB) is not less than 1 and absolute value of INI is not less than 1. By DV bounds Initial move = Initial Input Perturbation * Move Limit Fraction * (UB-LB). Default when initial value of input variable is zero. INI Initial input variable value LB, UB Lower and upper bounds on input variable
Move Limit Fraction	0.15	0.0 < Move Limit Fraction < 1.0	Move limit fraction. Note: Smaller values allow for a more steady convergence (smaller fluctuation of the output response values), but more computational effort could be consumed. The value will be adaptively updated during optimization process.
Initial Input Perturbation	1.1	≠0.0	Initial input variable perturbation value. Larger value result in wider spread of the initial N designs ( $n$ is the number of input variables; the $n$ designs together with the start design can determine a linear response surface). Adaptive Response Surface Method will search the design space more widely.
Constraint Screening (%)	50.0	real value	Constraint screening. > 0.0 Constraint is retained (not screened out) if it is violated or within the given percentage of its critical value (bound). < 0.0 As many constraints are retained as memory permits.
Max Failed Evaluations	20,000	>=0	When On Failed Evaluations is set to Ignore failed evaluations (1), the optimizer will tolerate failures until this threshold for Max Failed Evaluations. This option is intended to allow the optimizer to stop after an excessive amount of failures.
Minimal Move Factor	0.1	0.0 < Minimal Move Factor < Move Limit Fraction	Minimal move factor. It is to avoid too small of the step size. It is used in the initial sampling step (See Minimal Move Factor in Initial Linear Move) and also in the preceding move limit strategy.
Response Surface	SORS	SORS SRSM	SORS Uses the second order response surface (SORS). SRSM Uses the scalable response surface method (SRSM). When SRSM is used, the limit on Maximum Iterations >= N+2 should be deleted, where N is number of input variables. When there are a lot of input variables and the computational effort is limited, SRSM is a good choice.
Solver	SQP	MFD SQP Hybrid	The method Adaptive Response Surface Method uses to solve the response surface based optimization problem. Tip: It is recommended to use 2 when there are a lot of discrete variables.
Points per Iteration	1	>0	Controls the number of points used in an iteration after the first iteration. The number of points used per iteration can result in different iteration histories.
Sample Points	0	>=0	0 Automatically determined; in SRSM, Sample Points is set to $n$ . $n$ is the number of input variables. >0 Use the user defined value. Sample Points is useful only if Response Surface = 1.
Use SVD	No	No or Yes	Useful in case of soft convergence In case of soft convergence: No Adaptive Response Surface Method is terminated. Yes Singular Value Decomposition is activated to re-build the response surfaces, and the optimization process is continued.
Revision	A-multi	A B A-multi B-multi	Assists when there is a convergence difficulty. The B revision is less likely to become stuck if iterations do not exhibit successive improvement. By default, "A" is selected meaning the legacy algorithm. Note: A-multi and B-multi are new versions of A and B that support multi-execution. The classification of iteration points is different between A and A-multi (and B and B-multi).
Use Inclusion Matrix	With Initial	With Initial Without Initial	With Initial Runs the initial point. The best point of the inclusion or the initial point is used as the starting point. Without Initial Does not run the initial point. The best point of the inclusion is used as the starting point. Restart ARSM Used with existing data from an Adaptive Response Surface Method run with the same settings. Mainly used if the Optimization is terminated early or reached the limit on the number of evaluations. If the included data is not from an existing Adaptive Response Surface Method run, for example from a DOE, it can negatively effect the performance of Adaptive Response Surface Method.