Altair AcuSolve EDEM Coupling

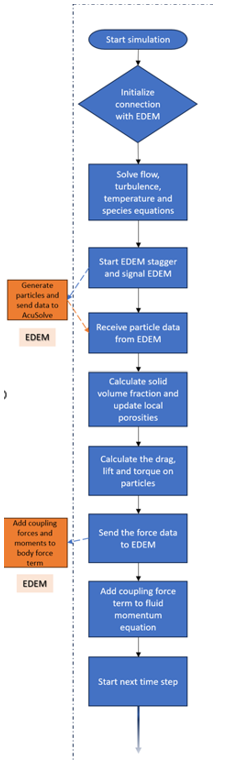
Note: The detailed DEM simulation sequence is not shown here. For detailed information about the DEM simulation sequence, refer to the EDEM help manual.

Note:

The temperature and species equations are only solved when the heat transfer and/or mass transfer physics models are active.
Since the DEM time step is usually multiple orders lower than the CFD time step, the DEM solver loop is repeated multiple times per single CFD time step to ensure that the physical time is synchronized in both the solvers.
For coupled simulations, the data is always exchanged in SI units.
For unidirectional coupling, once the coupling forces are calculated and shared with EDEM, the fluid momentum equation is not updated with the coupling force because the effect of particles on fluid is ignored.

AcuSolve-EDEM coupling uses the Eulerian-Lagrangian approach for modeling fluid-particle flows where the fluid transport equations are solved in a Eulerian framework and the dispersed phase is represented as Lagrangian particles. The fluid phase is solved based on the volume-averaged Navier-Stokes equations and the Discrete Element Method (DEM) is used for computing the motion of the solid phase. This coupling strategy allows you to study the momentum and heat transfer at the individual particle scale.

Governing Equations

The volume-averaged Navier-Stokes equations for CFD-DEM momentum coupling are given by:

\frac{\partial (ε_{f} ρ_{f})}{\partial t} + \nabla \cdot (ρ_{f} ε_{f} v_{f}) = 0

\frac{\partial}{\partial t} (ε_{f} ρ_{f} v_{f}) + \nabla \cdot (ρ_{f} ε_{f} v_{f} v_{f}) = - ε_{f} \nabla p - ε_{f} \nabla \cdot (τ_{f}) + ρ_{f} ε_{f} g - F_{p}

where,

$ε_{f}$ is the fluid volume fraction or porosity;
$v_{f}$ is the fluid velocity;
$ρ_{f}$ is the fluid density;
$p$ is the fluid pressure;
$τ_{f}$ is the viscous stress tensor;
$g$ is the gravity vector;
$F_{p} = \frac{1}{V_{c e l l}} \sum_{i} {(f^{d} + f^{l})}_{i}$ is the particle-fluid force exchange term;
$V_{c e l l}$ is the volume of fluid cell;
$f^{d}$ is the fluid drag force;
$f^{l}$ is the fluid lift force.

Note: Wherever applicable the following notations are used throughout the document. The subscript

f

denotes a fluid property,

p

denotes a particle property and

i

denotes that the calculation is done for an individual particle.

The drag force on each particle is given by:

f_{i}^{d} = β^{D} \frac{V_{p}}{d_{p}} (v_{s l i p})

$v_{s l i p}$ is the slip velocity ( $v_{f} - v_{p}$ )
$V_{p}$ is the particle volume
$d_{p}$ is the particle diameter

Where the formulation of the interphase momentum exchange coefficient ( $β^{D}$ ) varies based on the drag model. The drag models available in AcuSolve-EDEM coupling are listed below.

Drag Models

Ergun-Wen Yu
The momentum exchange coefficient for the Ergun Wen Yu drag model is given by,
$β_{E r g u n}^{D} = \frac{A (1 - ε_{f}) μ_{f}}{ε_{f} φ^{2} d_{p}} + \frac{B ρ_{f} | v_{s l i p} |}{φ} ε_{f} < 0.8$
$β_{W e n Y u}^{D} = \frac{3}{4} C_{d} ρ_{f} |v_{s l i p}| ε_{f}^{- 1.65} ε_{f} \geq 0.8$
Where, the coefficients A and B have a default value of 150 and 1.75 respectively and can be modified by you while specifying the model inputs. $v_{p}$ is the particle velocity and $d_{p}$ is the particle’s volume equivalent sphere diameter. $φ$ is the sphericity of the particle.
$C_{d} = \{\begin{matrix} \begin{array}{l} 0 {Re}_{i} = 0 \\ \frac{24}{{Re}_{i}} (1 + 0.15 {Re}_{i}^{0.687}) {Re}_{i} \leq 1000 \end{array} \\ 0.44 {Re}_{i} > 1000 \end{matrix}$
Here ${Re}_{i}$ is the particle Reynolds number and $C_{d}$ is the drag coefficient.
${Re}_{i} = \frac{ρ_{f} ε_{f} |v_{s l i p}| d_{p}}{μ_{f}}$
The Ergun-Wen-Yu model is one of the most widely used drag models and is recommended for most of the fluid-particle flows since it works well for both dense phase and dilute phase regimes. In this model, the Ergun equation is used for fluid volume fractions less than 0.8 and the Wen-Yu equation for fluid volume fractions greater than 0.8.
Di Felice
The momentum exchange coefficient for the DiFelice drag model is given by,
$β_{d i F e l i c e}^{D} = \frac{3}{4} C_{d} ρ_{f} |v_{s l i p}| ε_{f}^{(2 - χ)}$
$χ = \{\begin{cases} 0 {Re}_{i} = 0 \\ 3.7 - 0.65 e^{(- 0.5 {(1.5 - \log_{10} {Re}_{i})}^{2})} {Re}_{i} \neq 0 \end{cases}$
$C_{d} = \{\begin{cases} 0 {Re}_{i} = 0 \\ {(0.63 + 4.8 {Re}_{i}^{- 0.5})}^{2} {Re}_{i} \neq 0 \end{cases}$
Unlike the Ergun-Wen-Yu correlation, the Di Felice correlation is a monotonic function of Reynolds number and porosity and does not have the step change in drag force evaluation.
Beetstra
The momentum exchange coefficient for the Beetstra drag model is given by,
$β_{B e e t s t r a}^{D} = \frac{A μ_{f}}{ε_{f} d_{p}^{}} + \frac{B μ_{f} {Re}_{i}}{d_{p}^{}}$
$A = 180 (1 - ε_{f}) + 18 ε_{f}^{4} (1 + 1.5 \sqrt{(1 - ε_{f})})$
$B = \frac{0.31 (ε_{f}^{- 1} + 3 (1 - ε_{f}) ε_{f} + 8.4 {Re}_{i}^{- 0.343})}{1 + 10^{3 (1 - ε_{f})} {Re}_{i}^{2 ε_{f} - 2.5}}$
Rong
The momentum exchange coefficient for the Rong drag model is given by,
$β_{R o n g}^{D} = \{\begin{cases} \frac{150 (1 - ε_{f}) μ_{f}}{ε_{f} d_{p} φ^{2}} + \frac{3}{4} \frac{ρ_{f} |v_{s l i p}|}{φ} ε_{f} < 0.8 \\ \frac{3}{4} C_{d} ρ_{f} |v_{s l i p}| ε_{f}^{2 - σ - λ} ε_{f} \geq 0.8 \end{cases}$
where,
- $σ = 2.65 (ε_{f} + 1) - (5.3 - 3.5 ε_{f}) ε_{f}^{2} e^{[- \frac{{(1.5 - \log_{10} {Re}_{i})}^{2}}{2}]}$
- $λ = (1 - φ) (C - D e^{- 0.5 {(3.5 - \log_{10} {Re}_{i})}^{2}})$
- $C = 39 φ - 20.6$
- $D = 101.8 {(φ - 0.81)}^{2} + 2.4$
- $φ$ is the sphericity of the particle
Since the sphericity of the particle is considered while calculating the drag force, this model is strongly recommended for non-spherical particles compared to the other models available in AcuSolve.
Syamlal-O’Brien
The momentum exchange coefficient for the Syamlal-O’Brien drag model is given by,
$β_{S y a m l a l}^{D} = \frac{3}{4} \frac{C_{d} ε_{f} ρ_{f} |v_{s l i p}|}{v_{r, p}^{2}}$
where,
$C_{d} = \{\begin{cases} 0 {Re}_{i} = 0 \\ {(0.63 + \frac{4.8}{\sqrt{\frac{{Re}_{i}}{v_{r, p}}}})}^{2} {Re}_{i} \neq 0 \end{cases}$
$v_{r, p} = 0.5 (A - 0.06 {Re}_{i} + \sqrt{(0.0036 {Re}_{i}^{2}) + 0.12 {Re}_{i} (2 B - A) + A^{2}})$
$A = ε_{f}^{4.14}$
$B = \{\begin{matrix} 0.8 ε_{f}^{1.28} ε_{f} \leq 0.85 \\ ε_{f}^{2.65} ε_{f} > 0.85 \end{matrix}$
Wen-Yu
The momentum exchange coefficient for the Wen-Yu drag model is given by,
$β_{W e n Y u}^{D} = \frac{3}{4} C_{d} ε_{f}^{- 1.65} ρ_{f} |v_{s l i p}|$
Schiller Nauman
The momentum exchange coefficient for the Schiller Nauman drag model is given by,
$β_{S c h i l l e r}^{D} = \frac{3}{4} C_{d} ρ_{f} |v_{s l i p}|$
$C_{d} = \{\begin{cases} 0 {Re}_{i} = 0 \\ 24 (1 + 0.15 {Re}_{i}^{0.687}) {Re}_{i} \leq 1000 \\ 0.44 {Re}_{i} > 1000 \end{cases}$
The drag force calculated does not consider the effect of surrounding particles, that is, volume fraction is not accounted for, and hence this model is strictly valid only for dilute phase flows.

Non-Spherical Drag Coefficient Models

The effect of the particle’s shape can be taken into account by using non-spherical drag coefficient models. There are two types of models available in AcuSolve which are listed below. If the non-spherical drag coefficient model is set to none then the particles are assumed to be of spherical shape. But when the drag coefficient model is set to either of the models listed below, the drag coefficient in the drag models will be replaced by the non-spherical drag coefficient.

Isometric (Haider Levenspiel)

In this model the drag coefficient is a function of particle Reynolds number and sphericity. The instantaneous orientation of the particle is not considered. This type of model is applicable for particles with shapes closer to a sphere, such as rocks and some grains (beans), and when the orientation of the particles is not critical. The user inputs required for this model are particle’s volume and sphericity. The Haider-Levenspiel correlation is given by:

C_{d}^{n s} = \frac{24}{{Re}_{c}^{}} [1 + A_{1} {({Re}_{c}^{})}^{A_{2}}] \frac{A_{3}}{(1 + \frac{A_{4}}{{Re}_{c}^{}})}

{Re}_{c} = \min ({Re}_{i}, 2.5999 e 5)

Where the constants A_1-4 are dependent on the sphericity (

φ

) of the particle.

Table 1.
$φ < 0.67$	$0.67 \leq φ < 0.99999$	$φ \geq 0.99999$
$\begin{array}{l} A_{1} = e^{(2.3288 - 6.4581 φ + 2.4486 φ_{}^{2})} \\ A_{2} = 0.0964 + 0.5565 φ \\ A_{3} = e^{(4.905 - 13.8944 φ + 18.4222 φ^{2} - 10.2599 φ^{3})} \\ A_{4} = e^{(1.4681 + 12.2584 φ - 20.7322 φ^{2} + 15.8855 φ^{3})} \end{array}$	$\begin{array}{l} A_{1} = 8.1761 e^{(- 4.0655 φ)} \\ A_{2} = 0.0964 + 0.5565 φ \\ A_{3} = 73.69 e^{(- 5.0748 φ)} \\ A_{4} = 5.378 e^{(6.2122 φ)} \end{array}$	$\begin{array}{l} A_{1} = 0.1806 \\ A_{2} = 0.6459 \\ A_{3} = 0.4251 \\ A_{4} = 6880.95 \end{array}$

Non-spherical (Ganser and Holzer-Sommerfeld)
The Ganser and Holzer-Sommerfeld models consider both the shape and orientation of the particle. Since the orientation of the particles is also considered, this model is applicable to particle shapes such as disk, ellipsoid and elongated cylinder. The user inputs for these models are volume and aspect ratio of the particles.
The Ganser correlation is given by:
$C_{d}^{n s} = \frac{24}{k_{1} {Re}_{i}^{}} [1 + 0.1118 {(k_{1} k_{2} {Re}_{i}^{})}^{0.6567}] + \frac{0.4305 k_{2}}{(1 + \frac{3305}{k_{1} k_{2} {Re}_{i}^{}})}$
Here $k_{1}$ and $k_{2}$ are Stokes and Newton shape factors respectively.
$k_{1} = \frac{1}{(\frac{ϕ_{p r o j}}{3} + \frac{2}{3 \sqrt{φ}})}$
$k_{2} = 10^{1.8148 {(- \log_{10} (φ))}^{0.5743}}$
Where $ϕ_{p r o j}$ is the particle’s projected diameter ratio and is dependent on the aspect ratio ( $A_{R}$ ) of the particle and the angle between the principal axis and the fluid velocity vector ( $α$ ).
$ϕ_{p r o j} = \{\begin{cases} \frac{\sqrt{\frac{4}{π} A_{R} \sqrt{(\sin^{2} α)} + \sqrt{(\cos^{2} α)}}}{{(\frac{3 A_{R}}{2})}^{\frac{1}{3}}} A_{R} = 1 \\ \frac{\sqrt{A_{R} \sqrt{(\sin^{2} α)} + \sqrt{(\cos^{2} α)}}}{{(A_{R})}^{\frac{1}{3}}} A_{R} \neq 1 \end{cases}$
Since this model only takes the aspect ratio as an input, the sphericity ( $φ$ ) is calculated from the aspect ratio using the following correlation:
$φ = \{\begin{cases} \frac{{(1.5 A_{R})}^{\frac{2}{3}}}{{(A_{R} + 0.5)}^{}} A_{R} = 1 \\ \frac{{(A_{R})}^{\frac{2}{3}}}{{(\frac{(1 + 2 A_{R}^{1.61})}{3})}^{}} A_{R} \neq 1 \end{cases}$
The Holzer-Sommerfeld correlation is given by:
$C_{d}^{n s} = \frac{8}{{Re}_{i}^{}} \frac{1}{\sqrt{φ_{}^{⊥}}} + \frac{16}{{Re}_{i}^{}} \frac{1}{\sqrt{φ_{}}} + \frac{3}{\sqrt{{Re}_{i}^{}}} \frac{1}{φ_{}^{\frac{3}{4}}} + {0.42}^{0.4 {(- \log_{10} φ_{})}^{0.2}} \frac{1}{φ_{}^{⊥}}$
Where sphericity is calculated from the aspect ratio using the correlation:
$φ = \{\begin{cases} \frac{{(1.5 A_{R})}^{\frac{2}{3}}}{{(A_{R} + 0.5)}^{}} A_{R} = 1 \\ \frac{{(A_{R})}^{\frac{2}{3}}}{{(\frac{(1 + 2 A_{R}^{1.61})}{3})}^{}} A_{R} \neq 1 \end{cases}$
$φ^{⊥}$ is the crosswise sphericity and is calculated as shown below:
$φ_{}^{⊥} = \{\begin{cases} \frac{π {(\frac{3 A_{R}}{2})}^{\frac{2}{3}}}{{(4 A_{R} \sqrt{(\sin^{2} α)} + π \sqrt{(\cos^{2} α)})}^{}} A_{R} = 1 \\ \frac{A_{R}^{\frac{2}{3}}}{{(A_{R} \sqrt{(\sin^{2} α)} + \sqrt{(\cos^{2} α)})}^{}} A_{R} \neq 1 \end{cases}$

Lift Models

Generally, the lift force acts in a direction normal to the relative motion of the fluid and particle. The two components of the lift force considered are Saffman force and Magnus force. The Saffman lift force is due to the pressure gradient on a non-rotating particle in the presence of a non-uniform shear velocity field while the Magnus lift force is due to the particle rotation in a uniform flow. Unlike spherical particles, the behavior of non-spherical particles in turbulent flows is much more complicated and the lift force acting on them can no longer be neglected. As the particle’s principal axis becomes inclined with the flow direction, the effect of lift force on the particle motion becomes significant.

The lift force on a particle is given by:

f_{i}^{L} = β_{l s}^{L} (v_{s l i p} \times ω_{f}) + β_{l m}^{L} (ω_{s l i p} \times v_{s l i p}) + β_{\ln}^{L} ({\hat{e}}_{L n})

Where,

$β_{l s}^{L}$ is the Saffman lift coefficient.
$β_{l m}^{L}$ is the Magnus lift coefficient.
$β_{\ln}^{L}$ is the non-spherical lift coefficient (used for non-spherical models only).
$ω_{f}$ is the curl of local fluid velocity ( $\nabla \times \vec{v_{f}}$ ).
$ω_{s l i p}$ is the curl of slip velocity ( $ω_{s l i p} = \frac{1}{2} ω_{f} - ω_{p}$ ).
$ω_{p}$ is the curl of particle velocity ( $\nabla \times \vec{v_{p}}$ ).

There are three lift models available in AcuSolve:

Saffman-Magnus
This model is for spherical particles and hence the orientation is neglected whereas the last two models take the particle orientation into account while calculating the lift forces.
The correlation for the Saffman force is given by:
$β_{l s}^{L} = S L C \times C_{l s} d_{p}^{2} \sqrt{μ_{f} ρ_{f}} {|ω_{f}|}^{- 0.5}$
SLC is Saffman constant with a default value of 1.615. This value can be modified by you while specifying the model inputs. $C_{l s}$ is given by the expression:
$C_{l s} = \{\begin{matrix} e^{- 0.1 {Re}_{i}} + 0.3314 \sqrt{γ_{i}} (1 - e^{- 0.1 {Re}_{i}}) {Re}_{i} \leq 40 \\ 0.0524 \sqrt{γ_{i} {Re}_{i}} {Re}_{i} > 40 \end{matrix}$
$γ_{i} = \frac{|ω_{f}| d_{p}}{2 |v_{s l i p}|}$
The correlation for the Magnus force is given by:
$β_{l m}^{L} = \frac{M L C \times C_{l m} {|v_{s l i p}|}^{2} π d_{p}^{2} ρ_{f}}{|ω_{s l i p}| |v_{s l i p}|}$
$ω_{s l i p} = \frac{1}{2} ω_{f} - ω_{p}$
MLC is Magnus constant with a default value of 0.125. This value can be modified by you while specifying the model inputs. $C_{l m}$ is given by the expression:

For the Saffman Magnus model, $β_{\ln}^{L}$ is always equal to zero.
Saffman-Magnus non-spherical lift
The non-spherical version of the Saffman-Magnus lift model is similar to the spherical lift model except the non-spherical lift coefficient ( $β_{\ln}^{L}$ ) is not equal to zero and is calculated as shown in the next section.
Non-spherical lift
When the non-spherical lift model is selected, the Saffman and Magnus lift coefficients are set to 0 and the non-spherical lift coefficient is assumed to be proportional to the drag coefficient and the correlation is given by:
$β_{\ln}^{L} = \frac{0.125 C_{D} (\sin^{2} α \cdot \cos α) π d_{p}^{2} {|v_{s l i p}|}^{2}}{|x^{'} \cdot v_{s l i p}| |(x^{'} \times v_{s l i p}) \times v_{s l i p}|}$
Here the drag coefficient is obtained from the drag force calculation and $α$ is the angle between the particle’s principal axis and the slip velocity vector. The direction of the lift force is given by:
${\hat{e}}_{L_{o}} = ({x^{'}}_{i} \cdot v_{s l i p}) ((x^{'} \times v_{s l i p}) \times v_{s l i p})$
where, ${x^{'}}_{i}$ is the particle principal axis and $v_{s l i p}$ is the slip velocity vector.

Torque Models

By using the torque models, the rotational drag force on the rotating particles due to the inertia of fluid can be considered. When AcuSolve sends the force information to EDEM, this torque is added to the rotational motion equation in EDEM. The torque on a particle is given by,

T_{i} = β_{r o t}^{T} (0.5 ω_{f} - ω_{p}) + β_{p i t c h}^{T} ({x^{'}}_{i} \times (f_{i}^{d} + f_{i}^{l}))

The three types of torque models available in AcuSolve are pitching torque, rotational torque and a combination of both.

Pitching torque
When the center of pressure of the force acting on a non-spherical particle does not coincide with the center of mass, it results in a hydrodynamic pitching torque, also known as offset torque, that acts around the axis perpendicular to the plane of relative fluid velocity and particle orientation vector. The pitching torque can change the angle of incidence of the particle.
The expression used for calculating the pitching torque coefficient is given by:
$β_{p i t c h}^{T} = 0.25 δ_{A R} (1 - {(\sin α)}^{3})$
$δ_{A R} = \{\begin{cases} 0.5 d_{p} {(A R)}^{\frac{2}{3}} A R > 1 \\ 0.5 d_{p} {(A R)}^{\frac{- 1}{3}} A R \leq 1 \end{cases}$
Where, $A R$ is the aspect ratio of the particle and $α$ is the angle between the particle’s principal axis and the slip velocity vector. When the pitching torque model is selected, the rolling torque coefficient is set to 0 and vice versa.
Rotational torque
A particle experiences rotational torque, also known as rolling friction torque, when there is a difference between the local fluid rotation and the angular velocity of the particle. The rotational torque is applied at the center of mass of the particle and the rotational torque coefficient is given by the expression:
$β_{r o t}^{T} = \frac{ρ_{f}}{2} {(\frac{d_{p}}{2})}^{5} c_{r} |0.5 ω_{f} - ω_{p}|$
$c_{r} = \{\begin{cases} 0 {Re}_{r} = 0 \\ \frac{64 π}{{Re}_{r}} {Re}_{r} \leq 32 \\ \frac{12.9}{{Re}_{r}^{0.5}} + \frac{128.4}{{Re}_{r}} 32 < {Re}_{r} < 1000 \end{cases}$
Where, ${Re}_{r}$ is the Rotational Reynolds number of the particle and is given by,
${Re}_{r} = \frac{ε_{f} ρ_{f} d_{p}^{2} |0.5 ω_{f} - ω_{p}|}{μ_{f}}$
Pitching rotational torque
When the pitching rotational torque model is selected, both pitching torque and rotational torque are applied on the particle.

Heat Transfer Governing Equations

When heat transfer is active, in addition to the momentum equation, the energy conservation equations for the fluid and the particle are solved simultaneously to obtain the temperature of each phase. The governing equations for obtaining the temperatures of the particles and fluid are described below:

\frac{\partial}{\partial t} (ρ_{f} ε_{f} C_{p f} T_{f}) + \nabla . (v_{f} ρ_{f} ε_{f} C_{p f} T_{f}) = \nabla . (ε_{f} k_{f} \nabla T_{f}) + Q_{p}

Where $Q_{p}$ represents the heat source term resulting from the heat transfer from the particle.

Q_{p} = \sum_{i = 0}^{N_{p}} h_{f p} A_{p} (T_{f} - T_{p})

$A_{p}$ is the surface area of the particle, $T_{p}$ is the particle temperature and $T_{f}$ is the fluid temperature. The heat transfer coefficient ( $h_{f p}$ ) is calculated using the empirical correlation given by ${Nu}_{p} = \frac{h_{f p} d_{p}}{k_{f}}$ where the Nusselt number is calculated using the following expression:

{Nu}_{p} = \{\begin{cases} 2 + 0.6 ε_{f}^{3.5} {Re}_{i}^{0.5} \Pr^{0.333333} {Re}_{i} < 200 \\ 2 + 0.5 ε_{f}^{3.5} {Re}_{i}^{0.5} \Pr^{0.333333} + 0.02 ε_{f}^{3.5} {Re}_{i}^{0.8} \Pr^{0.333333} 200 \leq {Re}_{i} < 1500 \\ 2 + 0.000045 ε_{f}^{3.5} {Re}_{i}^{1.8} Re \geq 1500 \end{cases}

Where $Pr$ is the Prandtl number given by $Pr = \frac{μ_{f} C_{p f}}{k_{f}}$ .

The rate of change of the particle’s temperature over time is given by,

m_{p} c_{p} \frac{d T}{d t} = \sum_{}^{} Q_{h e a t}

Where $Q_{h e a t}$ is the sum of conductive and convective heat fluxes. The convective heat flux is calculated by AcuSolve based on the correlation described above and shared through the coupling interface once per each AcuSolve time step. The conductive heat transfer is due to particle-particle and particle-geometry contacts and is calculated based on the relative temperatures and the particle overlap. The conductive heat flux between two particles $p 1$ and $p 2$ is given by,

Q_{p 1 p 2} = \frac{4 k_{p 1} k_{p 2}}{k_{p 1} + k_{p 2}} {[\frac{3 F_{N} r^{*}}{4 E^{*}}]}^{1 / 3}

Where $k$ is the thermal conductivity, $F_{N}$ is the normal force, $r^{*}$ is the geometric mean of the particles’ radii and $E^{*}$ is the effective Young’s modulus for the two particles.

Mass Transfer Model

The governing equations for the mass transfer in AcuSolve-EDEM coupling are described below:

\frac{\partial (ε_{f} ρ_{f})}{\partial t} + \nabla \cdot (ρ_{f} ε_{f} v_{f}) = \overset{•}{m}

Additionally, a species transport equation is also solved for tracking the transport of the vapor phase in the fluid domain.

\frac{\partial}{\partial t} (ρ_{f} ε_{f} ψ_{v}) + \nabla . (v_{f} ρ_{f} ε_{f} ψ_{v}) = \nabla . (D_{v} \nabla ψ_{v}) + \overset{•}{m}

\frac{\partial}{\partial t} (ρ_{f} ε_{f} C_{p f} T_{f}) + \nabla . (v_{f} ρ_{f} ε_{f} C_{p f} T_{f}) = \nabla . (ε_{f} k_{f} \nabla T_{f}) + Q_{p}

For the mass transfer simulations, the heat source term on the right-hand side consists of both the convective term and a latent heat term due to evaporation of the liquid phase, that is, moisture content of particle. This is calculated as shown below:

\frac{d T_{p}}{d t} = f_{2} \frac{N u}{3 \Pr} (\frac{θ_{1}}{τ_{p}}) (T_{f} - T_{p}) + (\frac{L_{V}}{C_{p, l}}) \frac{\overset{•}{m}}{m}

Where the first term on the RHS represents the convective term and is scaled by an augmentation factor due to the evaporation of liquid and the second term represents the latent heat effects. $θ_{1}$ is the ratio of heat capacity of the carrier gas to that of the liquid phase of the evaporate.

$\overset{•}{m}$ is the rate of evaporation of the liquid content and is given by,

\overset{•}{m} = \frac{d m}{d t} = - \frac{S h}{3 S c_{f}} (\frac{m}{τ_{p}}) H_{M}

Where,

$S h$ is the Sherwood number given by $S h = 2 + 0.6 ε_{f}^{3.5} {Re}_{i}^{0.5} S c_{f}^{0.333333}$ .
$S c_{f}$ is the Schmidt number defined as $S c_{f} = \frac{μ_{f}}{ρ_{f} D_{f}}$ , $D_{f}$ is mass diffusivity of the fluid.
$H_{M}$ is the evaporation potential which is analogous to the temperature difference for heat transfer.
$m$ is the liquid mass on each particle.

Stokes flow time constant of the particle, $τ_{p} = \frac{ρ_{l} d_{p}^{2}}{18 μ_{f}}$

The evaporation potential $(H_{M})$ , also known as the specific driving potential for mass transfer, is calculated as shown below:

H_{M} = \log (1 + B_{M})

$B_{M}$ is the Spalding transfer number for mass given by,

B_{M} = \frac{ψ_{s, e q} - ψ_{f}}{1 - ψ_{s, e q}}

ψ_{s, e q} = \frac{χ_{s, n e q}}{(χ_{s, n e q} + (1 - χ_{s, n e q}) (\frac{W_{m o l, f}}{W_{m o l, v}}))}

χ_{s, n e q} = χ_{s, e q} - (\frac{2 L_{K}}{d_{p}}) β_{e v a p}

β_{e v a p} = - (\frac{3 \Pr τ_{p}}{2}) (\frac{\overset{•}{m}}{m})

L_{K} = \frac{μ_{f} \sqrt{2 π T_{p} (\frac{\bar{R}}{W_{m o l, l}})}}{S c_{f} p_{f, l o c a l}}

χ_{s, e q} = (\frac{p_{a t m}}{p_{f, l o c a l}}) e^{((\frac{L_{v} W_{m o l, v}}{\bar{R}}) (\frac{1}{T_{b, v}} - \frac{1}{T_{p}}))}

f_{2} = \frac{β_{e v a p}}{(e^{β_{e v a p}} - 1)}

Where,

$ψ$ is the mass fraction of vapor and $χ$ is the mole fraction of vapor. The subscript $s$ represents the vicinity of the particle, $f$ represents the free stream, $e q$ represents equilibrium and $n e q$ represents the non-equilibrium species fractions. $W_{m o l, f}$ is the molecular weight of the carrier gas and $W_{m o l, l}$ is the molecular weight of the liquid phase of the evaporate. $L_{v}$ is the latent heat of vaporization of the liquid, $T_{b, v}$ is the liquid boiling temperature, $T_{p}$ is the particle temperature. $\bar{R}$ is the universal gas constant, $p_{a t m}$ is the standard atmospheric pressure and $p_{f, l o c a l}$ is the local fluid pressure.