Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Steady State AC Magnetic: solved equations (vector model 2D)
Introduction
The vector model is the general model proposed for 2D applications.
Equation solved with vector model (2D applications)
The Maxwell-Faraday equation ![]() implies presence of electric scalar potential V, such as:
implies presence of electric scalar potential V, such as: ![]()
The equation solved by the finite elements method in a Steady State AC Magnetic application is written:
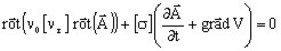
The complex image of this equation ( ![]() is replaced by
is replaced by ![]() ) is the
following equation:
) is the
following equation:
![]()
where:
- [νr] is the tensor of the reluctivity of the medium
- ν0 is the reluctivity of the vacuum; ν0 = 1/μ0 = 1/(4 π 10-7) (in m/H)
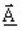 is the magnetic
vector complex potential (in Wb/m)
is the magnetic
vector complex potential (in Wb/m)- [σ] is the tensor of the conductivity of the medium (in S)
- V is the electric scalar potential (in V)
State variables, vector model (2D)
The state variables are:
- the
magnetic vector complex potential
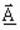
- the electric scalar potential V
The state variables, dependent on the problem type, plane 2D or axisymmetric 2D, are given in the table below.
| Type of the problem | State variable |
Notation (in Flux 3D) |
|---|---|---|
| plane | An | AN2* |
| axisymmetric | r.An | RAN2 |