Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Surface impedance condition (3D)
Introduction
For a 3D application where the skin effect is pronounced, it is recommended to use the surface impedance formulation.
What is this about?
The surface impedance condition is a particular boundary condition, which takes into account the conducting volume regions solely by their boundaries, in the case when the skin effect is pronounced.
The surface impedance condition imposes a relation
between the electric field ![]() and the magnetic
field
and the magnetic
field ![]() at the surface of the conducting region.
at the surface of the conducting region.
Hypothesis
A hypothesis is created of a null electric field
![]() throughout the conductor, except for the surface of
the conducting region, where a surface current density
throughout the conductor, except for the surface of
the conducting region, where a surface current density ![]() exists.
exists.
Definition
The surface impedance (![]() )
relates the tangential component of the magnetic field with the tangential component of
the electric field at the surface of the conducting region, using the following
relation:
)
relates the tangential component of the magnetic field with the tangential component of
the electric field at the surface of the conducting region, using the following
relation:
![]() , with
, with ![]()
where:
-
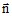 is the unity vector
normal to surface and exiting from the conducting region
is the unity vector
normal to surface and exiting from the conducting region - the index “s” signifies points placed on the surface of the conducting
region, where the electric and magnetic fields are tangential.
Validity and limitations
There exist the following limitations for using the surface impedance condition:
- limitation of topological order: connectivity problem
- limitation of geometric order: The value of the skin depth δ must be small with respect to the conductor dimensions:
- δ <<L, where L is the significant length or width of the conducting region
- δ <<r, where r is the significant curvature radius of the conducting region
This limitation can be written as: δ <L/5 and δ < r/5
-
limitation of physical order:
The field must be mainly tangent to the surface of the conducting region (negligible normal components of the field at the surface).
This limitation can be written: δ /L>10(μ0/μ) and μ >10μ0
Interest
This formulation is a very economical one and it provides reliable results.
Description of the solid conductor region
A conducting region with a pronounced skin effect is defined using: Region of solid conductor type described by surface impedance
A conducting region described by surface impedance is the combination of:
- an inactive volume region
- the boundary of the region on which the impedance surface condition is applied
The magnetic field is tangent to the boundary.
The state variable(s) are not computed on the internal nodes of the volume region (inactive). Therefore, it is not necessary to mesh this region.
Boundary conditions
Similarly, it is possible to apply the surface impedance condition on the computation domain boundary (of thin region type).