Explanation of results: Flux and Inductance (theoretical)

Flux: definition

Consider a surface S placed in a magnetic field . The flux of the magnetic flux density across the surface S is written: .

Magnetic flux across a random surface

For a surface perpendicular to the flux and a homogeneous flux density on the surface the result is: .

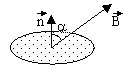
For a surface whose normal is oriented randomly with respect to the flux density, the elementary magnetic flux is: .

Thus, the flux across a random surface will be the surface integral:

In 3D, if the surface is in contact with two regions modeled by different magnetic scalar potentials, the results on each side of the surface can be different. This is explained by the fact that the modeling with scalar potentials does not ensure definitively the continuity of the normal component B_n of the magnetic flux density, but it ensures that of the tangential component H_t of the magnetic field intensity (unlike the vector model that ensures the local continuity of B_n, but not that of H_t).

Flux in a coil

In the case of a coil having N turns, the magnetic flux across the coil has the expression:

where:

is the magnetic flux “seen” by a turn and

is the total magnetic flux in the coil, “seen” by N turns

We can compute the flux within a coil by computing the flux across a surface corresponding approximately to the coil geometry. This method is not accurate, but can be sufficient, in particular for a mutual flux computation. Other methods of magnetic flux computation are presented in the next paragraphs.

Self-inductance of a coil

The self-inductance of a coil k passed by a current I_k and crossed by the total magnetic flux Φ_k is given by the relation:

that for a linear problem can be written in the form:

Mutual inductance between two coils

The mutual inductance between two coils j and k is given by the relation:

which for a linear problem can be written in the form:

where:

• Φ_j is the magnetic flux in the coil j (non-supplied)
• I_k is the current in the coil k