Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Scalar quantities, phasor concept
Introduction
The available quantities for post-processing can be scalar or vector quantities.
This section deals with the scalar quantities and recalls several definitions: rotating vector, complex image, phasor…
Rotating vector, complex image
A sinusoidal time varying scalar quantity of pulsation ω can be geometrically represented by a vector rotating at the angular velocity ω.
This vector is the geometric representation of a complex number.
Example: sinusoidal current and complex image
Let there be a sinusoidal time varying current i(t) of ![]() amplitude, of ω
pulsation (ω = 2 π f) and of β phase at the time t = 0.
amplitude, of ω
pulsation (ω = 2 π f) and of β phase at the time t = 0.
The instantaneous value of this current, i : i = Î.sin(ω.t + β)
is equal to the imaginary part of the complex number i : i = Im(i)
|
Rotating vector with ω velocity |
Sinusoidal quantity i(t) of period T=2 π/ω |
|---|---|
The complex instantaneous value of a sinusoidal current is given by the following relation:
- under a cartesian form: i = Î.cos(ω.t + β) + j.Î.sin(ω.t+ β)
- under an exponential form: i = Î.e j(ω.t+ β)
where:
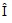 is the modulus of the
complex value i
is the modulus of the
complex value i- ωt + β is the argument (or the phase) of the complex value i
- β is the initial phase
Complex notation of a rotating vector
The rotating vector assigned to the sinusoidal quantity ![]() is expressed under the form
of a complex number A. This complex number can be written:
is expressed under the form
of a complex number A. This complex number can be written:
- under a
carthesian form:
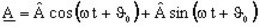
- under an
exponential form:
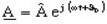
Phasor concept
The complex function ![]() associated to the sinusoidal quantity A(t) can be decomposed into two factors as
follows:
associated to the sinusoidal quantity A(t) can be decomposed into two factors as
follows:
![]()
This decomposition is presented in the table below.
| The factor … | which can be written … | Corresponds to a … |
|---|---|---|
|
|
|
rotating vector associated to the quantity A(t) at t = 0 |
|
|
|
vector rotation by an angle ωt |
- The factor
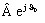 contains information
concerning the amplitude and the initial phase of the
quantity
contains information
concerning the amplitude and the initial phase of the
quantity 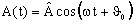
- The
factor
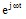 contains the
information concerning the time variation of the quantity
contains the
information concerning the time variation of the quantity
Phasor concept
The sinusoidal function in the time domain ![]() can be represented in the complex domain by the phasor
can be represented in the complex domain by the phasor
![]() .
.
Phasor: definition
We call ![]() the phasor
assigned to the quantity
the phasor
assigned to the quantity ![]() , i.e the phasor associated to the quantity
, i.e the phasor associated to the quantity ![]() is the rotating vector associated with this quantity at a
time t=0.
is the rotating vector associated with this quantity at a
time t=0.