Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Magneto-mechanical coupling: solving principle
Magneto mechanical coupling
The magneto-mechanical coupling takes into account the magnetic and kinematic aspects of a problem. The magnetic aspect is characterized by Maxwell's equations and the kinematic one by the fundamental equations of dynamics in translating or rotating motion.
Equations in electro magnetism
The equations used for the computation are repeated below:
- Maxwell's equations in electromagnetism:
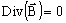
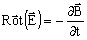

- other equations:

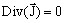
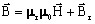
Fundamental dynamics equation in translating motion
The dynamics of a body in translating motion is expressed by the fundamental equation:
where:
- m is the mass of the moving body
- y is the instantaneous body position and ÿ is its linear acceleration
- Fr is the resistant mechanical force acting on the body
- Fem is the electromagnetic force acting on the body
Fundamental dynamics equation in rotating motion
The dynamics equation for the rotating motion of a body is:
where:
- J is the moment of inertia of the rotating body
- θ is the body's angular position and
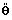 is its angular acceleration
is its angular acceleration - Γr is the resistant mechanical torque acting on the body
- Γem is the electromagnetic torque acting on the body
Solving principle
The magneto-mechanical coupling is a weak coupling between the electromagnetic and kinematic aspects of the problem. To solve this type of problem, we apply a four-stage procedure, as outlined below. At each time step, the electromagnetic aspect is analyzed first and then the kinematic one.
The algorithm of this method can be summarized as follows:
| Stage | Description |
|---|---|
| 1 | Solve the Maxwell equations and compute the electromagnetic force or torque acting on the moving part for a given relative position between the moving and fixed parts of the device |
| 2 | Solve the equation of moving part dynamics, compute the acceleration and speed of the moving part during a time step and compute the new position of the moving part for the next time step. |
| 3 | Move the moving part to the new position and (if necessary) re-mesh the displacement area. |
| 4 | Return to stage 1 for the next computation step |
Additional notes
The electromagnetic force and the magnetic torque acting on the moving part are computed by the virtual work method.
The mechanical force or torque acting on the moving part is an input data of the problem, entered by the user.