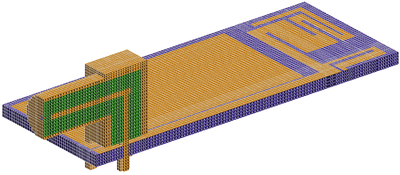
Finite Difference Time Domain (FDTD)
The finite difference time domain (FDTD) is a full wave time domain solution method, and Fourier transforms are applied to convert the native time domain results to the frequency domain.
The finite difference time domain (FDTD) solution technique has gained popularity in computational electromagnetics (CEM). Much of this popularity comes from its relatively straightforward formulation, where electric and magnetic fields are computed on two offset rectilinear grids and marched in time. This approach allows for the use of central differencing to approximate Maxwell’s equations. It can achieve second-order accuracy using first-order numeric differentiation.
The solution method is best suited to problems that include highly inhomogeneous materials and is, therefore, a popular choice in biomedical applications for the modelling of human phantoms. It is also a highly efficient solution for wideband problems, and is well suited to analyse broadband antennas. A single FDTD simulation with a pulsed excitation can be used to characterise a wideband frequency response of an antenna.