Jetting Effect
- Being the normalized vector between the projection of the center of the element upon segment ( , ) and the center of element as shown in Figure 1.
- The angle between the vector and the vector .
- The distance between the center of the element and its projection of a point upon segment ( , ).
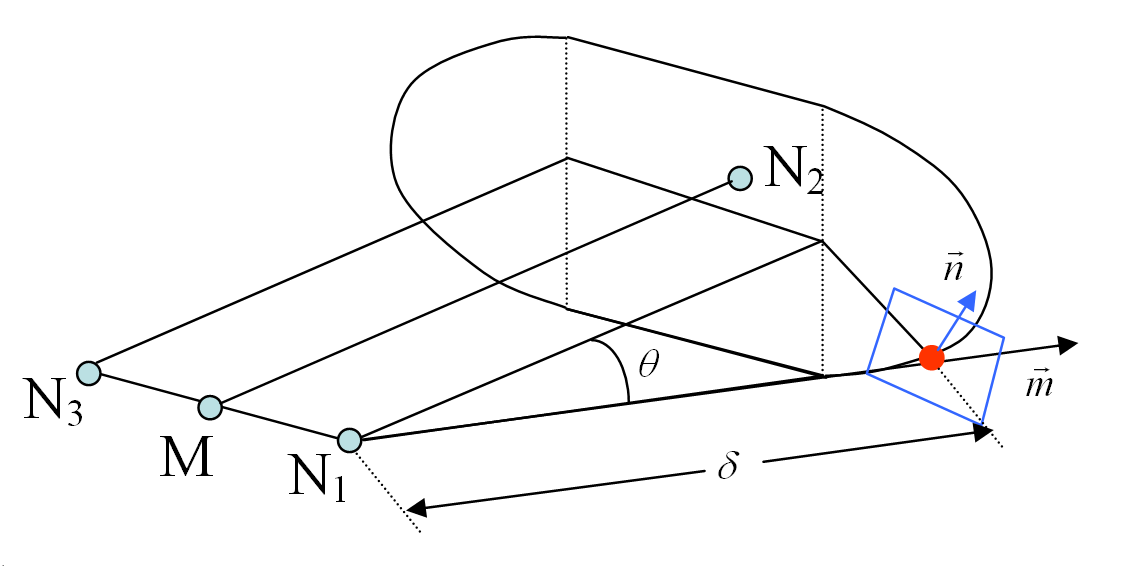
Figure 1. Jetting Effect Schema