/SKEW/FIX
Block Format Keyword Describes the fixed skew frames.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /SKEW/FIX/skew_ID/unit_ID | |||||||||
| skew_title | |||||||||
| Ox | Oy | Oz | |||||||
| X1 | Y1 | Z1 | |||||||
| X2 | Y2 | Z2 | |||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| skew_ID | Skew identifier This ID must be different from all frame (/FRAME/FIX) identifiers (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| skew_title | Skew title (Character, maximum 100 characters) |
|
| Ox | X coordinate of skew
origin O' (Real) |
|
| Oy | Y coordinate of skew
origin O' (Real) |
|
| Oz | Z coordinate of skew
origin O' (Real) |
|
| X1 | X component of skew
axis (Real) |
|
| Y1 | Y component of skew
axis (Real) |
|
| Z1 | Z component of skew
axis (Real) |
|
| X2 | X component of skew
axis (Real) |
|
| Y2 | Y component of skew
axis (Real) |
|
| Z2 | Z component of skew
axis (Real) |
Comments
- For fixed skews, the skew system is fixed and is defined by and . Vectors of arbitrary length may be given.
- For a fixed skew, inputs are
axis and
axis, but
axis is computed as:
(1) is recomputed as:(2) - The new fixed skew is defined by , and .
- The skew origin O' is useful when
defining some condition with respect to the skew in cylindrical coordinate system.
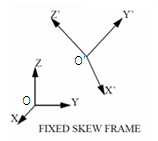
Figure 1.