Ogden Materials
Hyperelastic materials can be used to model the isotropic, nonlinear elastic behavior of rubber, polymers, and similar materials. These materials are nearly incompressible in their behavior and can be stretched to very large strains.
In Radioss, material laws LAW42, LAW62, LAW69, LAW82, and LAW88 utilize different strain energy density functions of the Ogden material model 1 to model hyperelastic materials. 2
Material Definition
- Engineering strain (also called nominal strain) in direction 1
- Stretch in direction 1
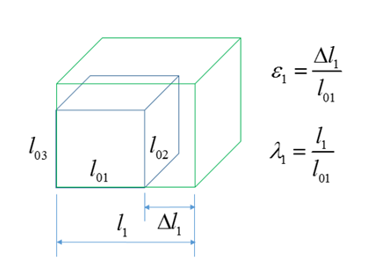
Thus, strain and stretch are related as:
Principal stretch can be used to describe the volumetric deformation by calculating the relative volume, , computed as:
- Uniaxial test:
and
- Biaxial test:
and
- Planar (shear) test:
and
/MAT/LAW42 (Ogden)
This material model defines a hyperelastic, viscous, and incompressible material specified using the Ogden, Neo-Hookean, or Mooney-Rivlin material models. This law is generally used to model incompressible rubbers, polymers, foams, and elastomers. This material can be used with shell and solid elements.
LAW42 uses the following strain energy density representation of the Ogden material model.
- Strain energy density
- ith principal engineering stretch
- Relative volume defined as:
- Deviatoric stretch
- and
- Material constants coefficient pairs.
The initial shear modulus and bulk modulus ( ) are given by:
and
Where, is the Poisson's ratio and is only used for computing the bulk modulus.
Material Parameters
Parameters and must be chosen so that initial shear modulus is:
For material stability, it is required that each material constant pair
In general, the Ogden model can be used for strains up to 700%. The number of terms material pairs, and , needed depends on the range of experimental data that is fit and curve fitting accuracy desired. In practice, 3 material pairs fit most data. If the material pairs are not known for a particular material, then a curve fit of uniaxial test data can be performed in Radioss using LAW69 or via separate fitting software.
Neo-Hookean Model
A simple case of the Ogden material model is the Neo-Hooken model represented using the following equation for the strain energy density function:
- The first invariants of the right Cauchy-Green tensor
- Material constant
This representation can be derived from the LAW42 Ogden strain energy density function when:
; , and
The Neo-Hookean model is a simple model that is typically only accurate for strains less than 20%.
Mooney-Rivlin Model
A slightly more complex case of the LAW42 Ogden material model is the Mooney-Rivlin model, which can be represented using the following equation for the strain energy density function:
- and
- The first and second invariants of the right Cauchy-Green tensor
- and
- Material constants
This representation can be derived from the LAW42 Ogden strain energy density function when:
, , , and
Mooney-Rivlin constants are available from a material supplier or testing company. If they are not available, then a curve fit of uniaxial test data can be performed in Radioss using LAW69 or via separate fitting software. The Mooney-Rivlin material law is accurate for strains up to 100%.
Poisson's Ratio and Material Incompressibility
If a material is truly incompressible, then . However, in practice is not possible to use because that would result in an infinite bulk modulus, an infinite speed of sound, and thus an infinitely small solid element Time Step.
The effect of different Poisson’s ratio input can be seen in Figure 2. The largest difference in the results is at higher amounts of strain. The results will match the test data better when but this results in a time step that is 4 times lower than . Thus, to balance the computation time and accuracy it is recommended to use for incompressible rubber material.
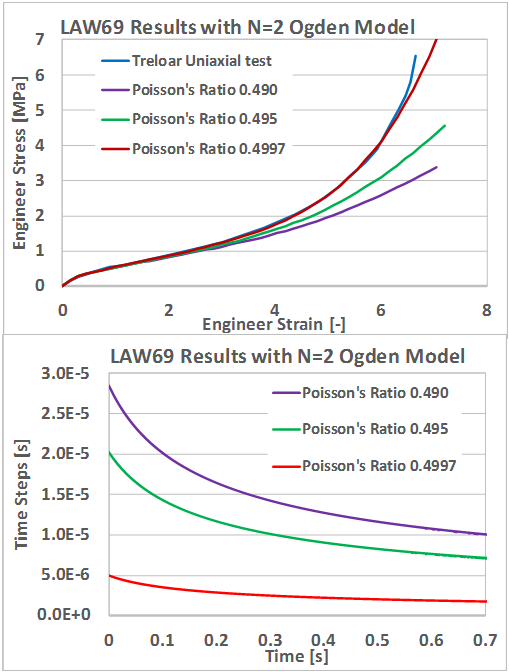
Higher values of the Poisson’s ratio may lead to a very small time step or divergence for explicit simulations.
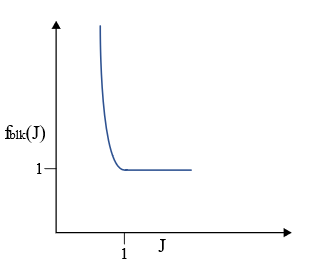
In LAW42, material incompressibility is provided by using a penalty approach, which calculates the pressure proportional to a change in density.
- Bulk modulus
- Relative volume which simplifies to relative density, if mass is constant
- Bulk coefficient scale factor versus relative volume function
- Abscissa scale factor for function
Viscous (Rate) Effects

The Maxwell model is represented using Prony series inputs ( ). The hyperelastic initial shear modulus is the same as the long-term shear modulus in the Maxwell model, and is the relaxation time:
The and values must be positive.
/MAT/LAW62 (VISC_HYP)
A hyper visco-elastic material law in Radioss that can be used to model polymers and elastomers.
The hyperelastic behavior in this material law is defined using the following strain energy density function:
- Strain energy density
- principal stretch
- Relative volume defined in Equation 13
- and
- Material constants coefficient pairs.
Viscous (Rate) Effects

The Maxwell model is represented using a Prony series with inputs. The initial shear modulus is:
The sum of should be greater than 0.
The stiffness ratio is:
With,
and the ground shear modulus
/MAT/LAW69
This law, like /MAT/LAW42 (OGDEN) defines a hyperelastic and incompressible material specified using the Ogden or Mooney-Rivlin material models. Unlike LAW42, where the material parameters are input, this law computes the material parameters using test data from a uniaxial engineering stress-strain curve.
This material can be used with shell and solid elements.
- law_ID = 1 (Ogden law):
- law_ID = 2 (Mooney-Rivlin
law):
Material Parameters
After reading the stress-strain curve (fct_ID1), Radioss calculates the corresponding material parameter pairs using a nonlinear least-square fitting algorithm. For the classic Ogden law, (law_ID=1), the calculated material parameter pairs are and where the value of p is defined via the N_pair input. The maximum value is N_pair=5 with a default value of 2. Usually no more than N_pair=3 is needed for a good fit.
For the Mooney-Rivlin law (law_ID =2), the material parameter and are calculated remembering that and for the LAW42 Ogden law can be calculated using this conversion:
, , , and
The minimum test data input should be a uniaxial tension engineering stress strain curve. If uniaxial compression data is available, the engineering strain should increase monotonically from a negative value in compression to a positive value in tension. In compression, the engineering strain should not be less than -1.0 since -100% strain is physically not possible.
- The experimental data curve represents a smooth monotonically increasing function with uniform distribution of abscissa points. The number of data points in the experimental data curve should be greater than the number of parameter pairs (N_pair).
- The engineering strain is negative in compression and positive in tension. For compression test data, the engineering strain should be greater than -1.0 (100% compression maximum) but tension only stress strain data can also be used.
- If N_pair ≥ 3, then the test data should cover at least 100% of the tensile strain and/or 50% of the compressive strain.
- N_pair should not be set to a very large value to avoid instabilities in the fitting procedure.
This material law is stable when (with =1,…5) is satisfied for parameter pairs for all loading conditions. By default, Radioss tries to fit the curve by accounting for these conditions (Icheck=2). If a proper fit cannot be found, then Radioss uses a weaker condition (Icheck=1:), which ensures that the initial shear hyperelastic modulus ( ) is positive.
To determine how well the calculated material parameters represent the input test data, the Radioss Starter outputs an “averaged error of fitting” value which is recommended to not exceed 10%. For visual comparison, the stress-strain curve calculated from the strain energy density and calculated material parameters is also output by the Radioss Starter.
Due to the friction involved in a uniaxial compression test, it is usually more accurate to take equal biaxial tension test data and convert it to uniaxial compressive data using these formulas 3 which are valid for incompressible materials.
- Uniaxial engineering compressive stain
- Equal biaxial engineering tension strain
- Uniaxial engineering compressive stress
- Equal biaxial engineering tension stress
Material Incompressibility
Material LAW69 uses the same method to maintain incompressibility as LAW42. For additional information, refer to Poisson's Ratio and Material Incompressibility in LAW42.
Viscous (Rate) Effects
/VISC/PRONY must be used with LAW69 to include viscous effects. Alternatively, LAW69 could be used to extract the Ogden or Mooney-Rivlin parameters and then those parameters can be used in LAW42 with viscosity added.
/MAT/LAW82
This material model defines a hyperelastic, and incompressible material specified using the Ogden, Neo-Hookean, or Mooney-Rivlin material models. This law is generally used to model incompressible rubbers, polymers, foams, and elastomers.
This material can be used with shell and solid elements. As compared to LAW42 or LAW62, this law uses a different Ogden strain energy density formulation given in Equation 26. The LAW82 strain energy density formulation matches what is used in some other finite elements solver’s hyperelastic model and; thus, the material parameters for this form of the Ogden strain energy density are sometimes available from material suppliers or other sources.
- Strain energy density
- Number of material constants , and
- Deviatoric stretch
- Relative volume as defined in Equation 2
The initial shear modulus:
- If , should be entered.
- If
,
input is ignored and will be recalculated
and output in the Starter output using:
- If and =0, a default value of is used and is calculated using Equation 28
Neo-Hookean Model
Like LAW42, LAW82 can also be simplified to a Neo-Hookean model by using:
, and
Mooney-Rivlin Model
Like LAW42, LAW82 can also be simplified to a Mooney-Rivlin model by using:
, , and
Viscous (Rate) Effects
/VISC/PRONY must be used with LAW82 to include viscous effects.
Drucker Condition Stability Check
In LAW42 and LAW69, the Drucker stability is automatically calculated by the Radioss Starter.
The Drucker stability condition checks if the change in the Kirchhoff stress corresponding to the infinitesimal change in the logarithmic strain (true strain) satisfies the following inequality.
Where, =1,2,3 principal direction.
- The change of Kirchhoff stress
- Relationship between Kirchhoff stress and logarithmic strain
The Drucker stability condition will be:
Here is tangential material stiffness matrix and it is also the slope of stress-strain curve:
For a stable material, it requests tangential material stiffness be positive (slope of stress-strain curve is positive). The tangential material matrix is positive if following conditions satisfied:
The Kirchhoff stress for Ogden model is:
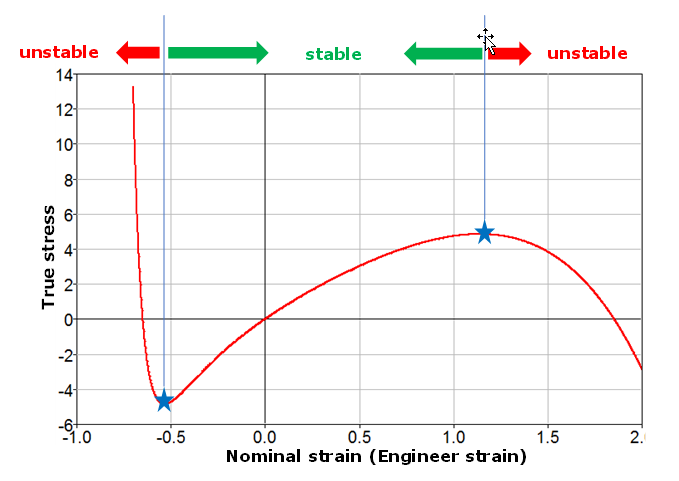
The Drucker stability criterion calculates the strain range where the material model will remain stable given a set of material parameters. This stability check cannot be made for every deformation but instead is commonly used to check material stability under uniaxial, biaxial and planar strain loading.
For example, using the following Ogden parameters:
CHECK THE DRUCKER PRAGER STABILITY CONDITIONS
-----------------------------------------------
MATERIAL LAW = OGDEN (LAW42)
MATERIAL NUMBER = 1
TEST TYPE = UNIXIAL
COMPRESSION: UNSTABLE AT A NOMINAL STRAIN LESS THAN -0.3880000000000
TENSION: UNSTABLE AT A NOMINAL STRAIN LARGER THAN 0.9709999999999
TEST TYPE = BIAXIAL
COMPRESSION: UNSTABLE AT A NOMINAL STRAIN LESS THAN -0.2880000000000
TENSION: UNSTABLE AT A NOMINAL STRAIN LARGER THAN 0.2780000000000
TEST TYPE = PLANAR (SHEAR)
COMPRESSION: UNSTABLE AT A NOMINAL STRAIN LESS THAN -0.3680000000000
TENSION: UNSTABLE AT A NOMINAL STRAIN LARGER THAN 0.5829999999999For a Mooney-Rivlin material, the Drucker stability should be checked since could be negative, which leads material instability.
/MAT/LAW88
This law utilizes a tabulated uniaxial tension and compression engineering stress and strain test data at different strain rates to model incompressible materials. It is only compatible with solid elements.
The material is based on the following Ogden’s strain energy density function but does not require curve fitting to extract material constants like most other hyperelastic material models. 4
Instead, this law determines the Ogden function directly from the uniaxial engineering stress strain curve tabulated data.
Unlike other Ogden material laws, the Bulk Modulus must be input from either test data or extracted from Starter output of the LAW69 Ogden curve fit. When comparing results between LAW42 or LAW69 to LAW88, the same bulk modulus must be used.
Unloading Behavior
Unloading can be represented using an unloading function or by providing hysteresis and shape factor inputs to a damage model based on energy.
If using the damage model, the loading curves are used for both loading and unloading and the unloading stress tensor is reduced by:
with
- Current energy
- Maximum energy corresponding to the quasi-static behavior
- and
- Input by user
- Tension
- Loading and Unloading
- = 0
-
Figure 7. 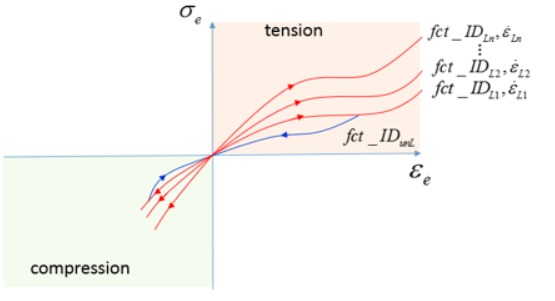
- = 1
-
Figure 8. 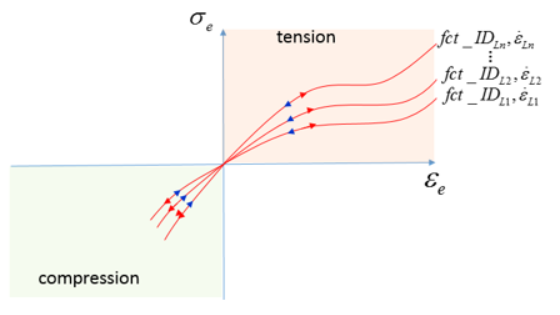
- = -1
-
Figure 9. 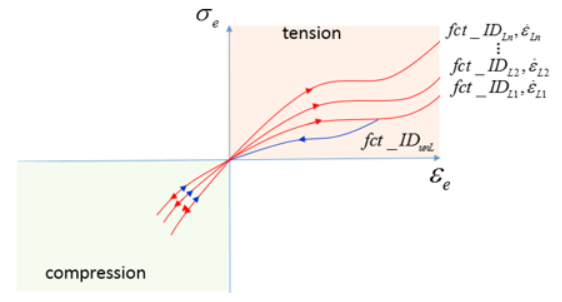
Viscous (Rate) Effects
Strain rate effects can be modeled by including engineering stress strain test data at different strain rates. This can be easier than calculating viscous parameters for traditional hyperelastic material models.
Conclusion
Make sure to use the material law that best fits the test data available.
For example, if minimum test data is available and the strains are not too large, the LAW42 Neo-Hookean model could be used. If the loading state is known, then it is important to have test data that represents that stress state and make sure the material model fits that test data.
References
http://www.axelproducts.com/downloads/TestingForHyperelastic.pdf