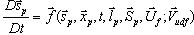Specifies the equation systems present in the problem.
Description
The
EQUATION command specifies the existence and types of the equation systems
and solution fields present in the problem. For example, to specify a problem with
particle position using the massless model and stretch, you
need:
EQUATION {
particle = massless
stretch = standard
}
while to use the finite mass model instead, you
need:
EQUATION {
particle = finite_mass
stretch = standard
}
In the massless model, the velocity of a particle always equals the flow velocity at the
particle's location. In the finite mass model, the particle velocity does not necessarily equal
the flow velocity. Instead, the particles have mass and are subject to forces such as drag and
gravity.
The massless particle and stretch equations are:
where
denotes the derivative in the particle frame of
reference, t is time,
is the particle position,
is the flow velocity,
is the transpose of the velocity gradient, and
is the stretch vector.
If the parameter
turbulence_trace in the
TRACE_PARAMETERS
command is set to on, the massless particle equation solved is not the above but
instead
where
is a random perturbation to the particle velocity
based on the eddy viscosity.
The finite mass particle equations are
where
is the particle velocity,
is the particle mass, and
is the sum of the forces acting on the particle. If
the parameter
turbulence_trace in the
TRACE_PARAMETERS command is set to on, then the values of
used in evaluating
are replaced by
.
Note: Particles are assumed to be spherical of
constant (subgrid scale) size.
The particle and stretch equations can be augmented by one or more user equations. The user
equations can either be evolution equations of the form
where
is the set of user-defined particle variables in the
current equation,
is the set of user-defined variables from the other
user equations (if any),
is the set of flow variables, and
is the set of user equation parameters; or
evaluation equations of the form
The user equations present in the problem are specified by the
user_equations parameter. Each user equation specified by the
user_equations parameter must be defined by a
USER_EQUATION command.
For example, evolution equations
tparticle and
cparticle for
particle temperature and composition could be defined. To include these equations in
a problem, one could
have:
EQUATION {
...
user_equations = {tparticle, cparticle}
}
USER_EQUATION( "tparticle" ) {
user_function = "usrTparticle"
num_variables = 1
...
}
USER_EQUATION( "cparticle" ) {
user_function = "usrCparticle"
num_variables = 2 # 2 species example
...
}
The
EQUATION command specifies the existence and types of the equation systems
and solution fields present in the problem. The
TIME_SEQUENCE and
STAGGER commands must then be used to request the solution
for the specified equations. For example, to solve for particle position and
stretch, you could
have:
EQUATION {
particle = massless
stretch = standard
}
TIME_SEQUENCE {
staggers = { "particle", "stretch" }
...
}
STAGGER( "particle" ) {
equation = particle
...
}
STAGGER( "stretch" ) {
equation = stretch
...
}
As with
particle and
stretch equations, the
TIME_SEQUENCE and
STAGGER commands must be
used to request the solution for the specified user equations. For example, to solve
for particle position, temperature, and composition, you could
have:
EQUATION {
particle = massless
user_equations = {tparticle, cparticle}
}
TIME_SEQUENCE {
staggers = { "particle", "tparticle", "cparticle"}
...
}
STAGGER( "particle" ) {
equation = particle
...
}
STAGGER( "tparticle" ) {
equation = user_equation
user_equation = "cparticle"
...
}
STAGGER( "cparticle" ) {
equation = user_equation
user_equation = "tparticle"
...
}
USER_EQUATION( "tparticle" ) {
user_function = "usrTparticle"
num_variables = 1
...
}
USER_EQUATION( "cparticle" ) {
user_function = "usrCparticle"
num_variables = 2
...
}
If an equation is defined by the EQUATION command, but no active stagger references that equation, the solution field of that equation is unaltered throughout the analysis.
Particle components are a generalization of a marker variable; they can also be considered a
generalization of species or composition. When number_particle_components
is greater than zero, particle components are initialized in the
PARTICLE_SEED command. The values of the particle components are constant in
time but they may vary over the particles in the problem according to how they are
initialized.