Présence d'un plan de masse parfait
Introduction
En électronique de puissance, l'architecture générale des structures est telle que les pistes de connexion sont très souvent positionnées au-dessus d'un plan conducteur appelé plan de masse.
La proximité de ce plan conducteur a une influence sur la valeur des inductances partielles de ces pistes (inductance propre et inductances mutuelles) car des courants induits s'y développent.
Cet effet s'explique facilement par la méthode des images, comme cela est présenté dans les blocs suivants.
Méthode des images : principe
La méthode des images s'applique en présence d'un plan de masse parfait.
Un plan de masse parfait est un plan infini, infiniment conducteur (résistivité nulle)*.
Un conducteur situé à une distance d d'un plan de masse parfait peut être remplacé par deux conducteurs identiques, à une distance 2d.
Si le conducteur est // au plan de masse, le conducteur et son image sont parcourus par des courants égaux de sens opposés (cf. figure ci-dessous).
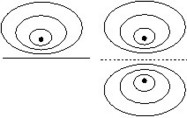
* En pratique, il suffit que le plan de masse dépasse à peine la superficie du circuit.
Méthode des images : mise en œuvre
En présence d'un plan de masse, les inductances partielles sont donc remplacées par des inductances partielles équivalentes pour tenir compte des conducteurs images.
La technique consiste à réécrire la tension aux bornes de chaque conducteur. Des exemples sont présentés dans les blocs suivants.
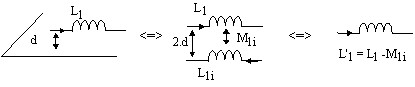
Inductance partielle d'un conducteur // au plan de masse
L'inductance propre équivalente d'un conducteur parallèle à un plan de masse s'écrit :
![]()
où :
- L1 est l'inductance propre du conducteur
- M1i est l'inductance mutuelle entre le conducteur et son image
Inductance partielle entre deux conducteurs // et // au plan de masse
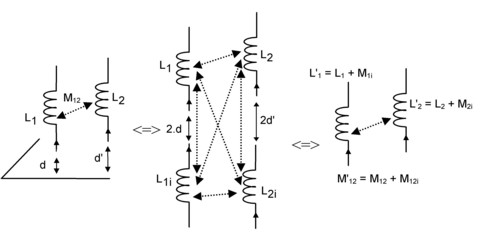
L'inductance mutuelle équivalente entre deux conducteurs parallèles entre eux et parallèles à un plan de masse s'écrit :
![]()
où :
- M12 est l'inductance mutuelle entre les deux conducteurs
- M12i est l'inductance mutuelle entre un des deux conducteurs et l'image de l'autre

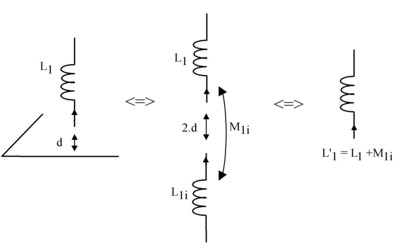
Inductance partielle d'un conducteur ⊥ au plan de masse
L'inductance propre équivalente d'un conducteur perpendiculaire à un plan de masse s'écrit :
![]()
où :
- L1 est l'inductance propre du conducteur
- M1i est l'inductance mutuelle entre le conducteur et son image
Inductance partielle entre deux conducteurs // et ⊥ au plan de masse
L'inductance mutuelle équivalente entre deux conducteurs parallèles entre eux et perpendiculaires à un plan de masse s'écrit :
![]()
où :
- M12 est l'inductance mutuelle entre les deux conducteurs
- M12i est l'inductance mutuelle entre un des deux conducteurs et l'image de l'autre