Cas réel : conducteurs volumiques
Introduction
Ce paragraphe donne l'expression analytique de l'inductance partielle dans le cas réel de deux conducteurs volumiques (section non nulle) parallèles. Cette expression est déduite de l'expression précédente par intégrations successives sur la largeur et l'épaisseur de chacun des conducteurs.
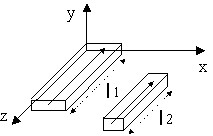
Rappel : L'inductance partielle entre les segments S1 et S2 s'écrit :
![]()
Hypothèses de calcul
Les hypothèses de calcul sont les suivantes :
- la densité de courant est uniforme dans la section droite des conducteurs
- les conducteurs sont des conducteurs à section rectangulaire
Obtention de la formule
La formule finale entre conducteurs volumiques est obtenue à la suite de quatre intégrations successives comme cela est présenté dans la figure ci-dessous.
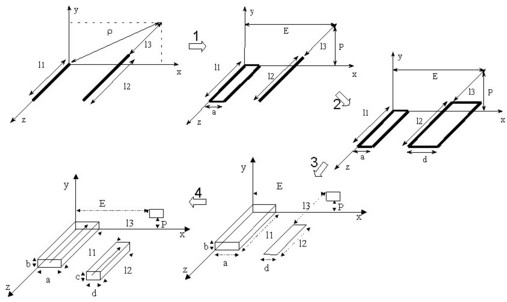
Selon la configuration géométrique des deux conducteurs, par exemple s'ils sont très éloignés, il est possible d'arrêter l'intégration à différents niveaux pour utiliser une expression moins lourde (intégration sur la largeur ou intégration sur l'épaisseur).
Inductance partielle entre deux conducteurs
Il s'agit de traiter le cas de l'inductance partielle entre deux conducteurs dans la configuration présentée ci-dessous.
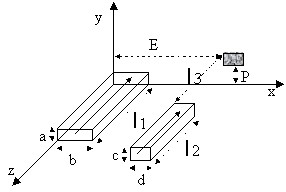
L'expression analytique ci-dessous donne la valeur de l'inductance mutuelle en µH si les distances sont exprimées en cm.
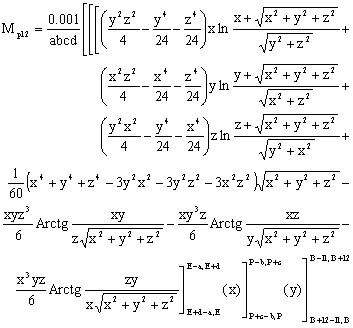
avec :
![]()
Inductance partielle d'un conducteur
L'inductance partielle d'un conducteur volumique est un cas particulier. Elle est obtenue en appliquant la formule précédente avec a = c, b = d, l1 = l2, l3 = 0, E = 0, P = 0.