Depuis la version 2026, Flux 3D et Flux PEEC ne sont plus disponibles.
Veuillez utiliser SimLab pour créer un nouveau projet 3D ou pour importer un projet Flux 3D existant.
Veuillez utiliser SimLab pour créer un nouveau projet PEEC (pas possible d'importer un projet Flux PEEC existant).
/!\ La documentation est en cours de mise à jour – des références au 3D peuvent subsister.
Magnéto Harmonique : équations résolues (modèle vecteur 2D)
Introduction
Le modèle vecteur est le modèle général proposé pour une application 2D.
Equation résolue en modèle vecteur (2D)
L'équation de Maxwell-Faraday : ![]() implique l'existence d'un potentiel scalaire électrique V tel
que :
implique l'existence d'un potentiel scalaire électrique V tel
que : ![]()
L'équation résolue par la méthode des éléments finis dans une application Magnéto Harmonique par la méthode des éléments finis s'écrit :
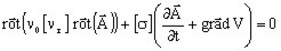
qui peut s'écrire avec la notation complexe (d/dt est remplacé par jω):
![]()
où:
- [νr] est le tenseur de réluctivité du milieu
- ν0 est la réluctivité du vide; ν0 = 1/μ0 = 1/(4 π 10-7) (en m/H)
-
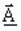 est le potentiel vecteur complexe magnétique (en
Wb/m)
est le potentiel vecteur complexe magnétique (en
Wb/m) - [σ] est le tenseur de conductivité du milieu (en S)
- V est le potentiel scalaire électrique (en V)
Variable d'état modèle vecteur (2D)
Les variables d'état sont :
- le
potentiel vecteur complexe magnétique
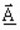
- le potentiel scalaire électrique V
La variable d'état, en fonction du type de problème (plan ou axisymétrique), est donnée dans le tableau ci-dessous.
| Type de problème |
Variable d'état |
Notation |
|---|---|---|
| plan | An | AN2* |
| axisymétrique | r.An | RAN2* |