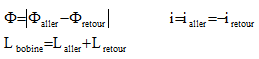Interprétations des résultats : calcul du flux réalisé par Flux
Rappel : lien EF/circuit
Voici un rappel sur les liens entre le domaine éléments finis et le circuit électrique :
| CIRCUIT | ELEMENTS FINIS |
|---|---|
| Dans le circuit électrique, on parle de : | Dans le domaine éléments finis, on parle de : |
| Composant de type conducteur bobiné |
Région de type conducteur bobiné ou Bobine non maillée (uniquement en 3D) |
| Composant de type conducteur massif | Région de type conducteur massif |
Disponibilités de calcul du flux
Le tableau ci-dessous permet de préciser les disponibilités de calcul du flux suivant la dimension et la méthode.
| 2D plan | 2D axi | 3D | ||
|---|---|---|---|---|
| Circuit | Calcul sur un composant de type conducteur bobiné |
|
|
|
| Calcul sur un composant de type conducteur massif |  |
|
|
|
| Eléments Finis | Calcul sur une région |
|
|
|
Calcul sur une région
La formule utilisée dans le logiciel Flux pour le calcul du flux sur une région est la suivante :
Flux : 
avec 
J : densité de courant
i : courant dans une spire
φ : flux à travers une spire
A : potentiel vecteur
S : aire de la région
V : volume de la région
n : nombre de spires
Calcul sur un conducteur bobiné en 2D
Le calcul du flux sur un conducteur bobiné en 2D est équivalent à la formule du calcul sur une région, détaillée dans la rubrique précédente.
La formule est appliquée sur toutes les régions auxquelles le conducteur bobiné est affectée.
Calcul sur un conducteur bobiné en 3D
Le calcul suivant est applicable pour le calcul du flux sur un conducteur bobiné en 3D uniquement.
Le conducteur bobiné peut être utilisé pour modéliser une bobine de type « courant imposé » ou « couplé circuit » :
- via une région de type conducteur bobiné
- via une bobine non maillée
Le flux Φk dans une bobine k s'exprime en dérivant la co-énergie magnétique Wm'par rapport au courant Ik dans cette bobine :
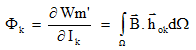
hok : champ créé par le bobinage k parcouru par 1A dans le vide
: domaine d'étude
La commande s'applique sur le composant électrique de type Conducteur bobiné et non directement sur une bobine car plusieurs bobines peuvent être regroupées par l'intermédiaire d'un composant (typiquement dans le cas de symétries et/ou périodicités).
Le flux calculé est un flux total (flux « embrassé » par un ensemble de spires), pour l'ensemble des bobines « appartenant » au composant électrique. Le nombre de spires est un nombre de spires total, c'est-à-dire la somme du nombre de spires de chacune des bobines.
Spécificité 3D sur les bobines non maillées : La précision du résultat dépend du maillage et en particulier du maillage autour des bobines. Pour une grande précision sur le flux, il peut être utile de décrire géométriquement et mailler les bobines. La précision du calcul est accrue avec des éléments du deuxième ordre.
Inductance : propre / mutuelle
Pour un modèle linéaire, après le calcul du flux, l'utilisateur peut en déduire l'inductance équivalente :
Si plusieurs bobines sont alimentées simultanément, l'inductance ainsi calculée est une inductance globale L qui inclut l'inductance propre de la bobine choisie L 11 et les mutuelles inductances dues aux autres bobines alimentées M12, M13...
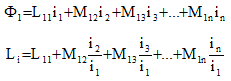
Pour calculer l'inductance propre d'une bobine, le courant dans les autres bobines doit être nul. Dans ces conditions, cette valeur peut aussi être obtenue en calculant l'énergie globale W du système :
Le flux à travers les bobines non alimentées (I2 = 0, I3 = 0, ...) permet d'en déduire leur mutuelle inductance avec celle qui est alimentée :
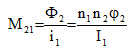
Le calcul de la matrice d'inductances d'un dispositif nécessite une résolution par bobine alimentée.
Inductance : règles de modélisation 2D
La modélisation d'une bobine est différente suivant le cas d'utilisation. Le calcul de l'inductance d'une bobine est donc différent suivant la modélisation mise en œuvre.
Le tableau ci-dessous permet de donner les informations nécessaires sur le calcul de l'inductance d'une bobine suivant la stratégie de modélisation utilisée :
| Déduction d'une inductance | Compléments | ||
|---|---|---|---|
| 2D plan | sans symétries / périodicités |
Si les régions aller et retour d'une bobine sont décrites, l'inductance de cette bobine est égale à la somme des inductances calculées sur les régions aller et retour :
|
Les régions aller et retour de chaque bobine doivent être alimentées simultanément afin que le dispositif étudié soit en état d'équilibre (intégrale des sources nulle).* |
| avec symétries / périodicités |
Si seulement la région aller d'une bobine est décrite en raison de symétries ou de périodicités, l'inductance de cette bobine est égale à deux fois l'inductance calculée sur la région aller :
|
En plan et sans boite infini, si seulement l'aller d'une bobine a été décrit en raison de symétries, le retour doit être obligatoirement simulé par des conditions aux limites. Si cette condition n'est pas réalisée les valeurs d'inductances obtenues peuvent être incorrectes. | |
| 2D axi |
L'inductance calculée sur une région est l'inductance de la bobine correspondante:
|
Une seule région est nécessaire pour décrire une bobine, soit une seule alimentation. Le dispositif est donc automatiquement en état d'équilibre. | |
Flux et symétries/ périodicités
Si le dispositif modélisé présente des symétries et/ou périodicités :
- Pour un calcul sur un composant, Flux prend en compte les bobines « originales » et
leurs « copies » par symétrie et/ou périodicité. Flux évalue pour ce calcul :
- le coefficient spécifique qui prend en compte le nombre et le type des symétries et/ou périodicités
- le champ Conducteurs en série ou en parallèle qui prend en compte le type d'association des conducteurs (tous en série, tous en parallèle).
- Pour un calcul sur une région, Flux calcul uniquement la grandeur sur la partie représenté sans tenir compte des symétries et ou périodicités. C'est dans ce cas à l'utilisateur d'appliquer le coefficient au résultat obtenu.