Equation résolue
Définitions
Considérons une surface élémentaire dS prise dans un milieu homogène, et traversée pendant le temps dt par une quantité de chaleur (ou énergie thermique) dQ.
On appelle flux de chaleur (ou flux thermique) élémentaire Φ la quantité de chaleur traversant la surface dS par unité de temps, soit : Φ = dQ/dt (en Watt).
La densité de flux de chaleur (ou densité de flux thermique) 
représente le flux de
chaleur par unité de surface ( φ s'exprime en W.m-2). Pour une
surface perpendiculaire au flux de chaleur φ = d Φ /dS.
Relations fondamentales
Les équations utilisées pour la résolution sont :
- la loi
de Fourier :
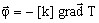(1) -
l'équation de la chaleur (Premier principe de la
Thermodynamique) :
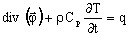(2)
où :
-
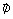est la densité de
flux de chaleur (en W/m2) - k est le tenseur de conductivité thermique (en W/m/K)
- ρCp est la capacité calorifique volumique (en J/m3 /K)
- q est la densité volumique de puissance thermique source (en W/m3)
Application de Thermique Permanent
Les conditions de calcul pour une application Thermique Permanent sont les suivantes : d/dt = 0 (régime permanent : la température ne varie pas en fonction du temps).
Dans ces conditions, les équations se résument de la façon suivante :
(1)
(2)
L'équation résolue par la méthode des éléments finis dans une application Thermique Permanent est l'équation suivante:
Application de Thermique Transitoire
Les conditions de calcul pour une application Thermique Transitoire sont les suivantes : d/dt ≠ 0 (régime transitoire ou régime variable : la température varie en fonction du temps).
Dans ces conditions, les équations se résument de la façon suivante :
(1)
(2)
L'équation résolue par la méthode des éléments finis dans une application de Thermique Transitoire est l'équation suivante:
Variable d'état
La variable d'état est la température (notée TKelvin et exprimée en Kelvin).