Conditions initiales et conditions aux limites

Introduction

Les équations précédentes permettent une description phénoménologique de la propagation de la chaleur dans un milieu homogène et isotrope. Les solutions physiquement intéressantes de ces équations sont celles qui tiennent compte des conditions initiales et des conditions aux limites du milieu considéré, c'est-à-dire à la frontière avec d'autres milieux.

Conditions initiales

Les conditions initiales peuvent être de type différent :

• Température uniforme dans tout le domaine d'étude
• Température non uniforme, c'est-à-dire températures différentes sur tous les noeuds du domaine d'étude (avec l'initialisation par solution EF *)

Conditions aux limites

Les conditions aux limites peuvent être de type différent :

• Température imposée sur la frontière :

  Une température T₀ est imposée sur la frontière. La température peut dépendre du temps et même varier le long de la frontière. Le cas le plus simple est T = T₀ = Cste sur toute la frontière.

• Densité de flux de chaleur 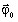imposée sur la frontière :

  Une densité de flux de chaleur 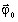est imposée sur la frontière (source de chaleur entrante ou sortante). Un cas particulier est φ₀ = 0, cela signifie que la paroi est isolée thermiquement (on dit aussi adiabatique). Il n'y a pas d'échanges thermiques avec le milieu extérieur.

• Transfert de chaleur avec le milieu ambiant :
  • transfert par convection : 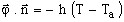, où :
    • h est le coefficient d'échange convectif en W/m²/K,
    • T_a est la température ambiante en K.
  • transfert par rayonnement à l'infini: 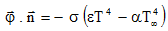, où :
    • ε est le coefficient d'émissivité,
    • σ est la constante de StephanBoltzmann ( σ = 5,675 · 10^-8 W/m² /K⁴)
    • α est le coefficient d'absorption
    • T_∞ est la température du corps virtuel avec lequel l'échange a lieu