Tools for the creation of the magnetic property B(H): specificities of the numerical models (splines)

Introduction

This section presents the creation of the magnetic property B(H) in the case of numerical models.

The main information refers to:

  • the description of the numerical models (standard spline and smoothed spline)
  • the operating mode for the creation of a magnetic property B(H) in the case of a numerical model

Two modes of description

It is possible to distinguish between two modes of description for the model:

  • the standard spline mode
  • the smoothed spline mode

Mode spline standard

In the standard spline mode, the curve B(H) is defined by the assembly of points entered by the user.

The user enters the pair of values B,H observing the following rules:

  • the pair of values B,H must respect an increasing sequence and begin with (0,0)
  • a sufficient number of points must be given to describe all the curve B(H) up to saturation (the number can vary from 4 to 200)
  • the last points must approximate an asymptote having the slope μ0
Note: It is advisable to display the dependence on H of the quantity μincremental(H) that permits the verification of the three validity rules quoted above. For a valid model, the curve is decreasing when H increases, and it inclines to the value 1 ad infinitum.

μincremental(H)

Smoothed spline mode

In the smoothed mode, the definition of the curve B(H) is simplified. This mode of definition requires fewer points than the standard spline mode.

The curve B(H) is divided into three parts:

  • the first part is a homographic function passing through zero and describing the bend of the B(H) dependence. It is defined by a pair of values (B,H) provided by the user and it ends at the last pair of values provided by the user
  • the second part is a homographic function for tangent connection to the first part and to the last part of the curve B(H)
  • the third part is a straight line of slope μ0, which intercepts the vertical axis (H = 0) at an ordinate corresponding to the saturation magnetic polarization Js

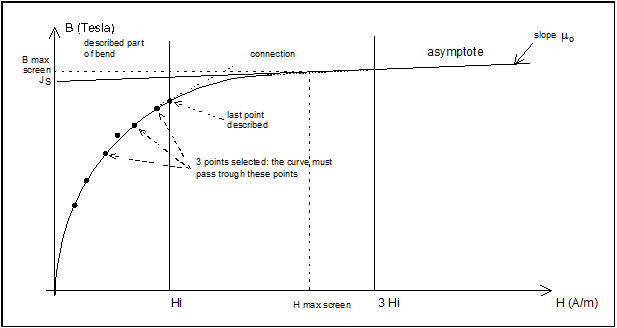
The user enters the pair of values B,H observing the following rules:
  • the pair of values (B,H) must respect an increasing order
  • the user must describe the first part of the B(H) curve, up to the bend, with:
    • 5 to 8 representative points
    • 3 points imposed on this curve
  • the user must enter the value of the saturation magnetic polarization Js in order to define the asymptotic part of the B(H) curve

Operating mode

To create a magnetic property B(H) with a numerical model, follow the operating mode below:

Step Action
1

In the my_base base of material

  • open the desired material my_mater
2

In the tab B(H)

  • click on Create magnetic properties
3

In the zone of the models

  • sort out the models by means of the proposed filters ⇒
  • choose the desired model:
    • spline isotropic saturation
    • spline anisotropic saturation
4

In the zone for the description of the model

  • click on the assistant (wizard)
→ Open the assistant …
External data / wizard
Step Action
1. External data

If the external data exist …

If not:

  • enter the pair of values (B,H)
  • choose the mode of construction:
    • smoothed spline (tick the box) ⇒ step 2
    • unsmoothed spline ⇒ step 3
  • click on Next
2. Smoothed spline

If smoothed spline:

  • choose the 3 points through which the curve B(H) passes
  • adjust the value of Js if necessary
  • click on Next
3. Synthesis Click on Next

External data …

Warning: It is important to note that for the numerical models (spline), there is synchronization between the external data and the initial points of the spline model (which are the model points for non smoothed spline).

The following table resumes what was described before:

Model Points (external data) Points (spline curve)
Standard spline The external data correspond to the points of passage of the curve (accessible and modifiable points) The points of the curve standard spline correspond to the external data (equality)
Smoothed spline The external data correspond to the initial points (accessible and modifiable points) The points of the smoothed spline curve correspond to the points calculated after the smoothening of the external data

Advice

If you work in the smoothed mode, you should not forget to tick the box at each modification.