Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Solved equation
Definitions
Let us consider an elementary surface dS in a homogeneous body, traversed by the heat quantity (or thermal energy) dQ during the time interval dt.
The elementary heat flux (or thermal flux) Φ related to the surface dS is the quantity of heat flowing through the dS surface during the unit of time, i.e., the ratio Φ = dQ/dt. The measurement unit of this quantity is Watt.
The vector quantity heat flux density (or thermal flux density) ![]() represents the heat flux
related to the unit of surface oriented in the direction normal to the surface. If the
heat transfer is perpendicular to the surface, the modulus of the heat flux density has
the expression φ = d Φ /dS. The measurement unit of φ is
W/m2.
represents the heat flux
related to the unit of surface oriented in the direction normal to the surface. If the
heat transfer is perpendicular to the surface, the modulus of the heat flux density has
the expression φ = d Φ /dS. The measurement unit of φ is
W/m2.
Basic relations
The basic relations of conduction heat transfer are:
-
the Fourier's law :
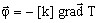 (1)
(1) -
the equation of heat conduction:
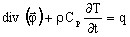 (2)
(2)
where:
-
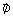 is the heat flux
density (in W/m2)
is the heat flux
density (in W/m2) - k is the tensor of thermal conductivity (in W/m/K)
- ρCp is the volumetric heat capacity (in J/m3/K)
- q is the volume density of power of the heat sources (in W/m3)
Steady state thermal application
In a steady state thermal application, d/dt = 0, i.e., the temperature field does not vary with respect to time.
Under these conditions, the previous relations can be reduced to:
![]() (1)
(1)
![]() (2)
(2)
The equation to be solved in a steady state thermal application is the following:
![]()
Transient thermal application
In the case of a transient thermal application (transient state or variable state) d/dt ≠ 0, and the temperature field is time dependent.
The corresponding relations are:
![]() (1)
(1)
![]() (2)
(2)
The equation to be solved in a transient thermal application is the following:
![]()
State variable
The state variable is the temperature (symbolized TKelvin and expressed in Kelvin).