Transient Electric: solved equations

Introduction

In a Transient Electric application the equations used for computation are:

• the corresponding Maxwell's equations for an electrical system, and

• the constitutive equation that characterizes the dielectric materials

The conditions of computation of a Transient Electric application are the following:

• the study is time depend: d/dt ≠ 0

the computation concerns the D and E fields; the B and H fields are not computed. The equations of the electric fields E, D and of the magnetic fields B, H are decoupled.

Equations and conditions

In the previously defined conditions of computation, the equations are summarized as follows:

Reminder about the differential operators:The curl divergence of a field is always null: [div rot (Field)] = 0.

Solved equation

The equation solved by the finite elements method in Flux in case of a Transient Electric application is the following:

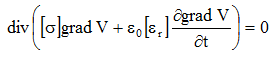
where:

• σ is the tensor of the conductivity of the medium (in Siemens),
• ε_r is the tensor of the relative permittivity of dielectric materials
• ε₀ is the vacuum permittivity; ε₀ = 1/(36 π 10⁹) (in F/m)
• V is the electric potential (in V)

State variable

The state variable in a Transient Electric application is the electric potential V (written Ve in Flux 3D).

The uniqueness condition of the electric potential V requires that the value of this potential at least in a point of the computation domain be known.