Since version 2026, Flux 3D and Flux PEEC are no longer available.
Please use SimLab to create a new 3D project or to import an existing Flux 3D project.
Please use SimLab to create a new PEEC project (not possible to import an existing Flux PEEC project).
/!\ Documentation updates are in progress – some mentions of 3D may still appear.
Closed magnetic circuit: magnetic connectivity problem (3D)
Introduction
This paragraph deals with the description of the closed magnetic circuits in 3D problems with the scalar model (automatic formulations).
Reminder about computation principle
To solve the equations in a Magneto Static application, two models are available:
- the vector model which uses the vector potential
- the scalar model which uses scalar potentials
In the scalar model (automatic formulations) there is no one equation that is solved by the finite elements method. Each region of the problem can have a specific formulation and, consequently, a specific equation. Thus, an interface exists between regions and, consequently, a coupling of formulations.
Connectivity problem
The coupling between the different potentials is sometimes forbidden in the sense that the hypotheses allowing the coupling between these potentials are no longer valid. This represents a connectivity problem.
Magnetic connectivity problem
The magnetic connectivity problem appears in the case of closed magnetic circuits of high permeability (transformers…). More precisely, it appears when there is a closed path passing through several volume magnetic regions and the line integral of H is not zero along this path.
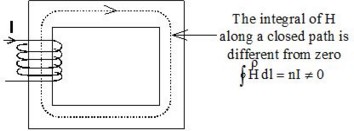
Solution: the cut concept
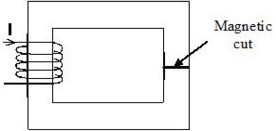
To overcome this problem, it is necessary that a cut be created in the magnetic circuit. This is a “mathematic cut” which means a jump in the scalar potential. The continuity of the fields B and H across the cut is obviously satisfied.
Practically, a cut is modeled by using a Magnetic cut entity.
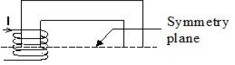
Symmetry and periodicity
It is not necessary to add a cut when the closed magnetic circuit is cut by a periodicity or symmetry plane
Examples
- example showing a connectivity problem
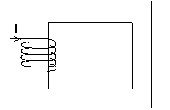
The magnetic circuit is closed
- examples without a connectivity problem …
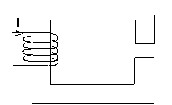
… because the magnetic circuit includes an air-gap
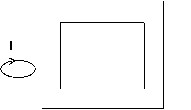
… because the current is “external” to the closed magnetic circuit