定义正交各向异性材料属性
用工程常数定义材料的正交各向异性属性。
格式
示例
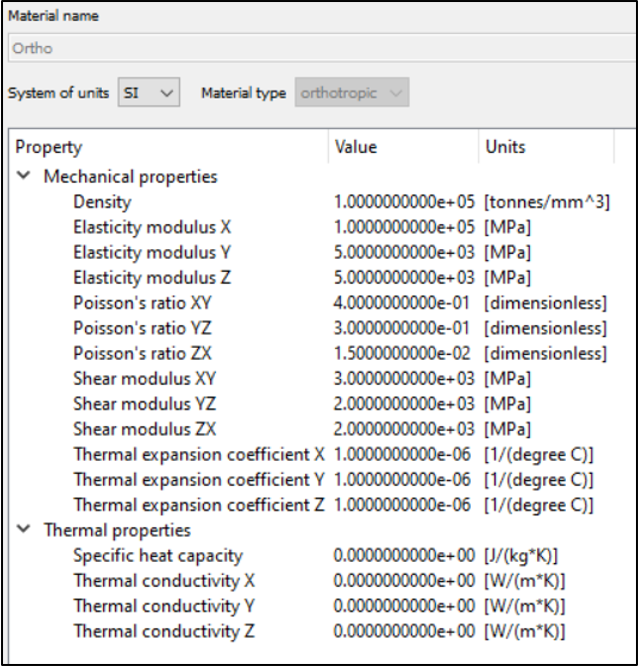
备注
- 正交各向异性材料具有三个相互垂直的对称面。正交各向异性线弹性材料的应力-应变关系可表示为:其中,柔度矩阵为 ,
Figure 3. 
Figure 4. 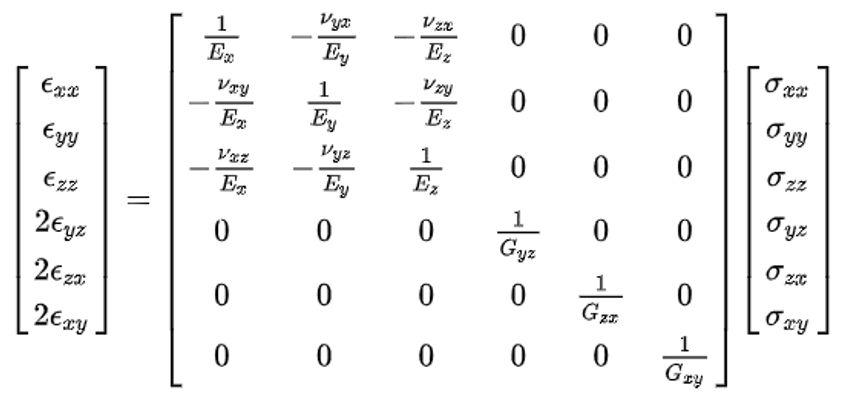
Figure 5. 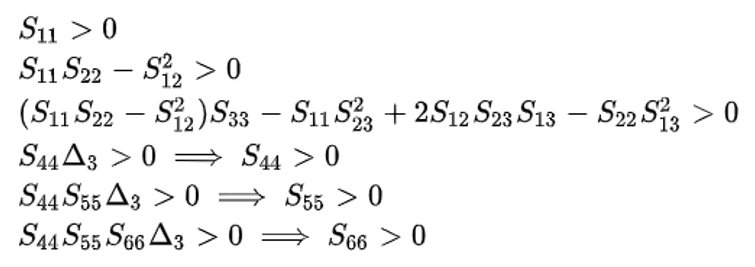
Figure 6. 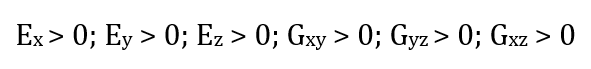
如果不满足上述条件,就会发生错误。Figure 7. 
- 如果热仿真需要,还可以给出热膨胀系数(沿 X、Y、Z 方向)和热属性。