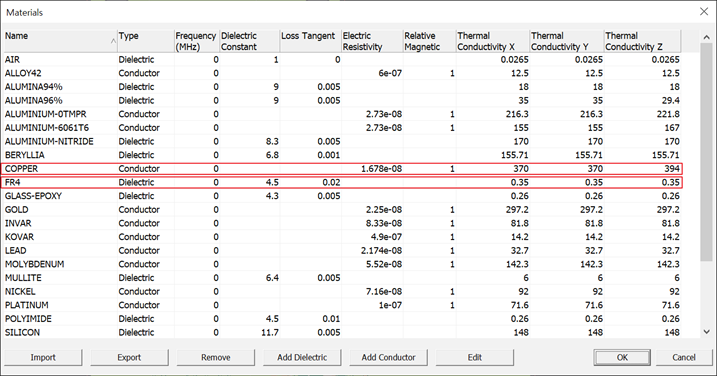
Setup Material Libraries
Manage material data.
- Manage Materials:
- Add, Modify, or Remove Materials: In the Material Manager dialog, you can add, edit, or remove materials.
- Export Materials: You can also export material data as a Material File (*.mtrl) for later use.
- Edit Materials:
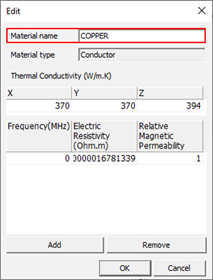
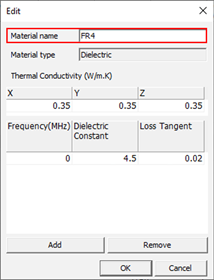
- To Modify a Material: Double-click on a material in the list, or select it and click Edit.
- To Add a New Material: Click Add Dielectric or Add Conductor to open the Edit dialog.
- Define Material Properties:
- Conducting Materials: Define the electric resistivity, relative magnetic permeability, and thermal conductivity for the x, y, and z axes.
- Dielectric Materials: Specify the dielectric constant, loss tangent, and thermal conductivity for the x, y, and z axes.
- Save and Load Material Files:
- Use the Import and Export buttons to save your material data to a file or load an existing material file.
 |
 |
| Property | Description |
|---|---|
| Conductivity |
Electrical conductivity or specific conductance is a measure
of a material's ability to conduct an electric current. When
an electrical potential difference is placed across a
conductor, its movable charges flow, giving rise to an
electric current. The conductivity
is defined as the ratio of
the current density J to the electric field strength
E:
It is also possible to have materials in which the conductivity is anisotropic, in which case is a 3×3 matrix (or more technically a rank-2 tensor), which is generally symmetric. Conductivity is the reciprocal (inverse) of electrical
resistivity,
, and has the SI units of
siemens per meter (S·m-1) and CGSE units of
inverse second (s–1):
|
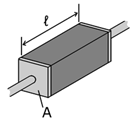
| Resistivity | Electrical resistivity
is defined as:
|
| Magnet Permeability | In electromagnetism, permeability is the measure of the
ability of a material to support the formation of a magnetic
field within itself. In other words, it is the degree of
magnetization that a material obtains in response to an applied
magnetic field. Magnetic permeability is typically represented
by the Greek letter μ. The reciprocal of magnetic permeability
is magnetic reluctivity. In SI units, permeability is measured in the henry per meter (H m-1), or newton per ampere squared (N A-2). The permeability constant (μ0), also known as the magnetic constant or the permeability of free space, is a measure of the amount of resistance encountered when forming a magnetic field in a classical vacuum. The magnetic constant has the exact value μ0 = 4π×10−7 ≈ 1.2566370614...×10−6 H·m-1 or N·A-2). |
| Thermal Conductivity | Thermal conductivity is the quantity of heat transmitted
through a unit thickness in a direction normal to a surface of
unit area, due to a unit temperature gradient under steady state
conditions. Thermal conductivity with heat transfer coefficients. 1 W/(mK) = 1 W/(moC) = 0.85984 kcal/(hr moC) = 0.5779 Btu/(ft hr oF) |
| Dielectric Constant | A dielectric is an electrical insulator that may be polarized
by the action of an applied electric field. When a dielectric is
placed in an electric field, electric charges do not flow
through the material, as in a conductor, but only slightly shift
from their average equilibrium positions causing dielectric
polarization. Because of dielectric polarization, positive
charges are displaced along the field and negative charges shift
in the opposite direction. This creates an internal electric
field which partly compensates the external field inside the
dielectric. If a dielectric is composed of weakly bonded
molecules, those molecules not only become polarized, but also
reorient so that their symmetry axis aligns to the
field. While the term "insulator" refers to a low degree of electrical conduction, the term "dielectric" is typically used to describe materials with a high polarizability. The latter is expressed by a number called the dielectric constant. A common, yet notable, example of a dielectric is the electrically insulating material between the metallic plates of a capacitor. The polarization of the dielectric by the applied electric field increases the capacitor's capacitance. |
| Loss Tangent | The loss tangent is a parameter of a dielectric material that quantifies its inherent dissipation of electromagnetic energy. The term refers to the angle in a complex plane between the resistive (lossy) component of an electromagnetic field and its reactive (lossless) component. |