Damping Models

Constant Damping Model

The linear damping force is computed according to the law:

Figure 1.

F = - c_{i} * v

Where:

c_i: Constant damping value, and is found in the [CONSTANT_DAMPING_xx] block for the i^th force direction in the property file.
v: Deformation velocity in the bushing in the i^th force direction.

Rubber Damping Model

Schematics and Equation

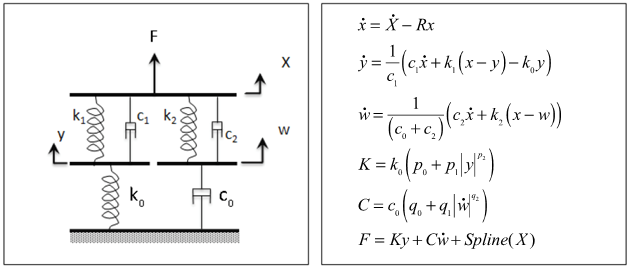
This model can be used for both dynamic and quasi-static tests.

The figure above-left shows a schematic of the bushing model where:

X: The input displacement provided to the bushing
y and w: The internal states of the bushing
k₀ and k₁: Represent the bushing rubber stiffness
k₂: Used to control the stiffness at large velocities
c₀: Produces the roll-off observed in the experimental data at low velocities
c₁: Accounts for the relaxation of the bushing impact force
c₂: Represents the viscous damping observed at large velocities

The governing equations for this bushing are shown above-right where:

R: The cutoff frequency associated with a first order filter that acts on the input X
x: The dynamic content of the bushing input X. This is the filter output.
$\dot{y}$ and $\dot{w}$: The time derivatives of the internal states of the bushing y and w
K: The effective stiffness of the bushing
C: The effective damping of the bushing
Spline (X): The static force response of the bushing.

The effective stiffness K and effective damping C are dependent on nonlinear effects such as friction in the bushing material and other nonlinear behavior that cannot be easily represented physically.

The effective stiffness K is k₀ multiplied by a factor:
Figure 3.

$S_{y} = (p_{0} + p_{1} {| y |}^{p^{2}})$
Similarly, the effective damping C is c₀ multiplied by a factor:
Figure 4.

$S_{w} = (q_{0} + q_{1} {| \dot{w} |}^{q^{2}})$

The total force generated by the bushing is the sum of 2 forces:

Static force at the operating point: Spline (X)
Force due to the dynamic behavior of the bushing: $K y + C \dot{w}$

First Order Filter

A first order filter, with cutoff frequency R, is used to identify the dynamic component, x, of the input signal, X. The transfer functions of the signal sent to the dynamic and the static models, assuming X0=0, are:

TF of signal to dynamic model=

$\frac{x (j ω)}{X (j ω)} = \frac{ω^{2}}{R^{2} + ω^{2}} + j \frac{R ω}{R^{2} + ω^{2}}, j = \sqrt{- 1}, ω = 2 π f = a n g u l a r f r e q u e n c y$

TF of signal to dynamic model=1

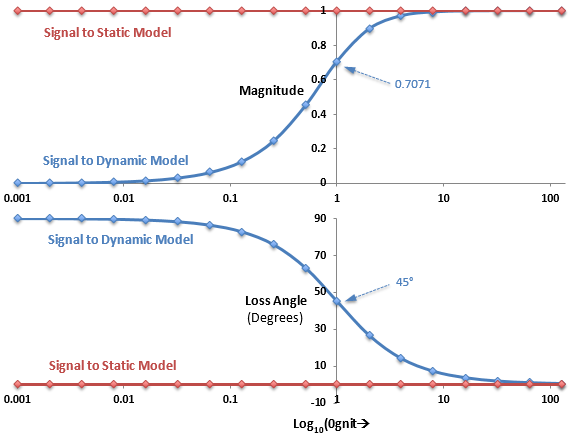
The following are Bode plots for these transfer functions:

The Bode plots show the magnitude and loss angle of the transfer functions over a range of operating frequencies:

The top figure plots the magnitude of the transfer function against Log₁₀(ω/R).
The bottom figure plots the loss angle of the transfer function against Log₁₀(ω/R).
Plots of the signal sent to the dynamic model are gray-blue.
Plots of the signal sent to the static model are brick-red.

The log scale used for the x-axis lets you view a wide range of frequencies and filter behavior as follows:

When (ω/R) << 1, that is at low frequencies, then:
- The magnitude of the signal sent to the dynamic model is close to 0.
- The loss angle of the signal sent to the dynamic model is close to 90°.
- The magnitude of the signal sent to the static model is 1.
- The loss angle of the signal sent to the static model is 0°.
The bushing essentially behaves as the static model. The loss angle of the signal sent to the dynamic model is close to 90°, but this is not important since the magnitude of the signal is close to zero.
When (ω/R) >> 1, that is at high frequencies, then:
- The magnitude of the signal sent to the dynamic model is close to 1.
- The loss angle of the signal sent to the dynamic model is close to 0° .
- The magnitude of the signal sent to the static model is 1.
- The loss angle of the signal sent to the static model is 0°.
The bushing essentially behaves as a dynamic model superimposed on top of a static model.
When (ω/R) = 1, that is at the cut-off frequency, then:
- The magnitude of the signal sent to the dynamic model is $1 / \sqrt{2 \approx 0.7071}$
- The loss angle of the signal sent to the dynamic model is 45°.
- The magnitude of the signal sent to the static model is 1.
- The loss angle of the signal sent to the static model is 0°.
The bushing essentially behaves as a dynamic model superimposed on top of a static model.

Scale Factors P0, P1, P2 and Q0, Q1, Q2

These factors are used to represent friction in the bushing material and also other effects such as viscoelasticity.

The overall scale factor is defined on the left for stiffness and on the right for damping as follows:

The following plot shows the behavior of the scaling function S_y for various values of

| y |

and _p₂. Note that the y-axis is plotted on a log scale to make the effects more obvious.

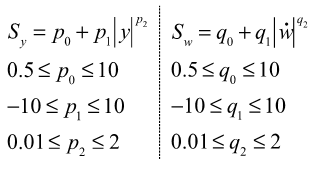
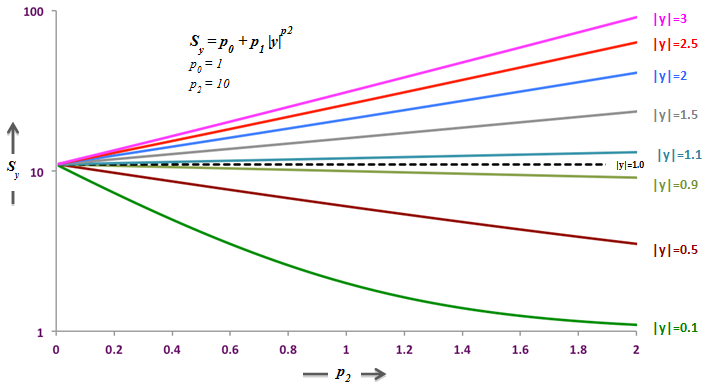
The functional form of S_y is selected as it easily represents a variety of shapes with very few parameters. Note that S_y and S_w are primarily responsible for capturing the dependency of the dynamic stiffness and loss angle on the amplitude of the input.

The next figure shows the same data as the figure above, except

| y |

is the x-axis and p₂ the curve parameter:

Multiple Preloads

The following equations show the method for computing the bushing output for multiple preloads.

Let:

n be the number of preloads in the test data; i be the current load case.
P_i be the preload corresponding to the i^th load case.
Sort the preloads P_i and renumber the preloads such that P₁ < P₂ < … < P_n.
_{x_i} be the filter output corresponding to the ith load case.
F0_i be the static response of the bushing corresponding to the i^th load case.
f_i be the dynamic response corresponding to the i^th load case.

Then for each preload, P_i, defines weights W_i:

And the total force is calculated as:

as you see detailed in the following figure:

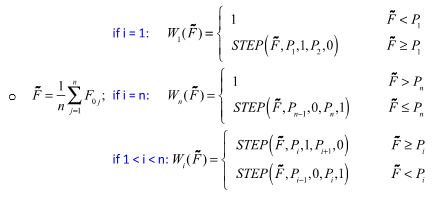
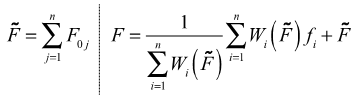
Factor RMIN

During simulation, an additional parameter RMIN is provided for you. If the fitted value of R is greater that RMIN, then the fitted value is used, otherwise RMIN is used. During run time, R affects how quickly the bushing responds to changes in the input.

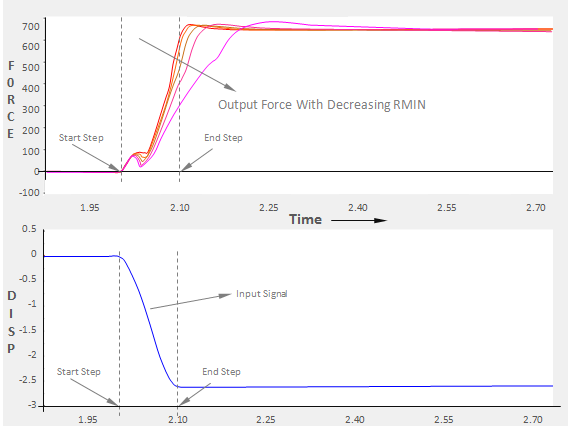
In the figure below, the displacement is given a step input at T=2.0 seconds. The displacement in the bushing changes from 0mm to -3mm between T=2.0 and T=2.1. The step input is stopped at T=2.10 seconds. The test is run with RMIN. What is observed is that as RMIN decreases, the bushing takes a longer time to respond to the input that is provided.

A large value of R implies that most of the signal is classified as steady state, so the static effects, which react instantaneously to input changes, will dominate. In contrast, when R is small, most of the signal is classified as transient. Therefore bushing internal dynamics will dominate the response and the response will be somewhat slower.

Lower Bound of R and RMIN Selection

The choice of a lower bound of R is essential to achieve a result that shows the correct characteristics for low frequencies and preload dependent simulations.

The lower bound you chose for R during fitting depends on how the bushing is going to be used during simulation and on the available test data. If the application isn’t known at the time of fitting, the lower bound may be chosen only according to the test data. In a concrete application that value of R can then be modified in the simulation model by setting RMIN accordingly.

Choosing the Lower Bound of R from the Test Data

The desired behavior for a bushing model is that input frequencies that are smaller than the lowest provided test frequency data f₀ be passed into the static spline. To achieve this behavior, the lower limit of R should be set greater or equal to 2f₀ $π$ .

Choosing the Lower Bound of R Based on Anticipated Usage During Simulation

If you desire that the simulation model have the ability to switch between two preloads within a given time $δ T$ , then you should choose R to be greater or equal to $\frac{2 π}{δ T}$

If you decide that these values of R are too conservative or you don’t want the entire response from the static spline, the simulation model is still capable of doing the switch between these preloads. The time it takes to complete a switch of all states from one preload to another is given by $\frac{2 π}{R}$ .

Hydromount Damping Model

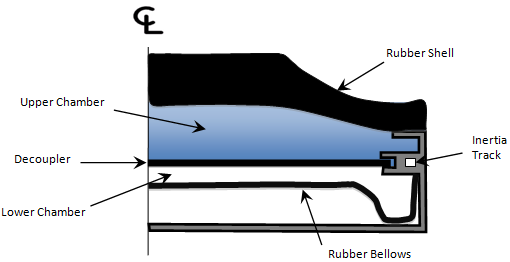
The following image shows a cross-section of a typical hydromount:

At low displacement amplitudes, fluid in the upper chamber simply deflects the decoupler. The hydromount behaves just like a rubber bushing. As the input displacement increases, the fluid in the upper chamber flows into the lower chamber. With increasing displacement, fluid effects start to dominate and the behavior of the hydromount changes dramatically.

The hydromount model therefore consists of two components: a rubber model and a fluid model. The total response of the hydromount is the sum of the rubber and the fluid effects. A cubic step function gradually turns on the fluid effects, so that transition from rubber behavior to full hydromount behavior is handled correctly. The following figure shows an equivalent mechanical model for the hydromount:

The governing equations for the hydromount model are as follows:

Inputs

X is the input displacement provided to the bushing.
R is the cutoff frequency associated with a first order filter.
The filter removes the steady state deformation of the bushing and passes only the transient portion of the input, x, to the dynamic models. The full input, X, is channeled to the static model.

Outputs

The total force generated by the bushing is the sum of three forces:

The force due to the fluid behavior, F_H, which is turned on gradually.
The force due to deformation in the rubber component, F_R.
The static force at the operating point, which is computed from the static spline that is provided.

X_R is a design parameter that defines the deformation at which the fluid force transition begins.

X_H is a design parameter that defines the deformation at which the fluid force transition ends.

Quite often, the test data for a hydromount does not capture the transition from pure rubber to full hydromount behavior. X_R and X_H are therefore not fitted, and are available for you to modify in the .gbs. The default values of X_R and X_H are such that the STEP function always returns 1.0.

For the fluid equations in the center:

z is an internal state representing fluid motion.
m_h represents the equivalent fluid mass.
k_h is the coupling stiffness between rubber and fluid.
c_h1 is the coupling damping between rubber and fluid.
c_h2 is the fluid damping.
j_o, j₁, j₂ and l₀, l₁, l₂ model the amplitude dependence in the fluid equations.
K_H is the effective fluid stiffness in the bushing.
C_H is the effective fluid damping in the bushing.

For the rubber equations in the center:

y and w are the internal states of the bushing.
k₀ and k₁ represent the bushing stiffness.
k₂ is used to control the stiffness at large velocities.
c₀ produces the roll-off observed in the experimental data at low velocities.
c₁ produces the roll-off observed in the experimental data at low velocities.
c₂ represents the viscous damping observed at large velocities.
p_o, p₁, ₂ and q_o, q₁, q₂ model the amplitude dependence in the rubber equations.
K is the effective stiffness of the bushing.
C is the effective damping of the bushing.

For the static equations on the right:

Spline (X) is the static force response of the bushing.

Filter implementation, multiple preload support, and the use of RMIN are exactly the same as for the rubber bushing.