Notion d'inductance partielle
Introduction
Si la notion d'inductance s'applique à une boucle fermée, chaque portion de cette boucle contribue à l'inductance totale. En 1972, A. E. Ruehli a introduit la théorie de l'inductance partielle, à la base de la méthode PEEC, qui permet de calculer la participation de chaque élément d'un circuit à son inductance totale.
Cette notion d'inductance partielle est présentée dans les blocs suivants.
Rappel
L'inductance d'une boucle de courant définie par un contour C, et parcourue par un courant I est le résultat de la circulation du potentiel vecteur A sur le contour C de cette boucle de courant.
![]()
Cette équation est valide dans les conditions suivantes :
- circuit filiforme dans lequel la densité de courant est constante
- absence de matériau magnétique dans la zone de champ créé par la boucle de courant
Principe
Prenons l'exemple simple d'une boucle de courant rectangulaire, où C = S1∪S2∪S3∪S4.
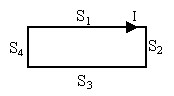
La circulation du potentiel vecteur A sur le contour C peut être décomposée sur chacun des quatre segments de la boucle rectangulaire.
![]()
De même, le potentiel vecteur en tout point peut être considéré comme la somme de la contribution de chacun des segments.
![]()
L'inductance de la boucle peut donc s'écrire sous la forme :
![]()
où ![]() est le potentiel
vecteur créé par le segment Sn.
est le potentiel
vecteur créé par le segment Sn.
Inductance partielle : définition
L'inductance de la boucle calculée précédemment peut également s'écrire sous la forme :
![]()
où MPmn représente l'inductance partielle entre les segments Sm et Sn
![]()
Pour m ≠ n, il s'agit d'une inductance mutuelle partielle MP
Pour m = n, il s'agit d'une inductance propre (ou self-inductance) partielle LP
Pour des portions parallélépipédiques de conducteurs en parallèles, des formules analytiques ont été développées : elles sont données dans la section § Formules analytiques.
Lorsque ces mêmes portions (ou éléments PEEC) sont positionnées en biais, des techniques d'intégration numériques doivent être employées pour le calcul de l'inductance mutuelle partielle. Plus de détails sont donnés dans la section § Formules semi-analytiques.
En revanche la mutuelle inductance entre deux conducteurs perpendiculaires est nulle.
Généralisation
Cette formulation n'est pas limitée au cas d'une boucle isolée. Elle peut être étendue à un système plus vaste.
En décomposant le système en portions élémentaires, on obtient ainsi une matrice d'inductances carrée, symétrique, dans laquelle les termes diagonaux correspondent aux inductances propres partielles et les termes non-diagonaux aux inductances mutuelles partielles.