Depuis la version 2026, Flux 3D et Flux PEEC ne sont plus disponibles.
Veuillez utiliser SimLab pour créer un nouveau projet 3D ou pour importer un projet Flux 3D existant.
Veuillez utiliser SimLab pour créer un nouveau projet PEEC (pas possible d'importer un projet Flux PEEC existant).
/!\ La documentation est en cours de mise à jour – des références au 3D peuvent subsister.
Interprétation des résultats
Courant de conduction et courant de déplacement
La densité de courant de conduction est donnée par le paramètre d'exploitation J2, qui correspond à la formule suivante :
La densité de courant total (courant de conduction et courant de déplacement) est donnée par le paramètre d'exploitation JT2, qui correspond à la formule suivante :
Puissances : aspect général
En ce qui concerne la puissance, il est possible de distinguer les grandeurs suivantes : la puissance apparente (S), la puissance active (P) ou la puissance réactive (Q). La puissance apparente complexe S s'écrit :
S = P + j Q
Dans Flux 3D, ces grandeurs s'expriment à l'aide des relations suivantes :
- la
densité de puissance apparente est donnée par la
formule :
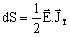qui
s'écrit :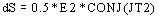 
- la densité de puissance active dP correspond à la partie
réelle de dS :
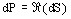qui s'écrit :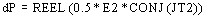 
- la densité de puissance réactive dQ correspond à la partie
imaginaire de dS :
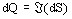qui s'écrit :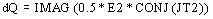 
Le calcul des grandeurs précédentes (puissance apparente (S), puissance active (P) ou puissance réactive (Q)) s'obtient avec la commande Intégrale (à l'aide des formules explicitées ci-dessus).
D'autres possibilités sont proposées à l'utilisateur pour le calcul de la puissance active et de la puissance réactive ; elles sont présentées dans les blocs suivants.
Puissance active
La densité de puissance active (valeur moyenne) en un point s'exprime à l'aide de E et j par la relation :
La puissance active (valeur moyenne) dans une
région volumique est égale à : 
Energie électrostatique
La densité d'énergie électrostatique (valeur moyenne sur une période) en un point s'exprime à l'aide de D et E par la relation :
qui peut également s'écrire, pour un
milieu linéaire, homogène, isotrope : 
L'énergie électrostatique (valeur moyenne sur une période) dans une région volumique est
égale à : 
Puissance réactive
La relation qui relie la densité de puissance réactive (dQ) et la densité d'énergie électrique (dWe) est la suivante : dWe=dQ/2ω
La puissance réactive dans une région volumique est directement égale à : Q=2ωWe