Concept of partial inductance
Introduction
The concept of inductance applies to a closed-loop contour. With respect to the line integral definition of the inductance, this total inductance can be considered as the addition of contributions of many contour segments. In 1972, A. E. Ruehli introduced the theory of partial inductance, which is the base of the PEEC method, which makes it possible to calculate the contribution of each element of a circuit to its total inductance.
This concept of partial inductance is presented in the following blocks.
Reminder
The inductance of a circuit closed-loop of current defined by a contour C and crossed by the electric current I, is the result of the line integral of the vector potential A on contour C of this loop of current.
![]()
This equation is valid under the following conditions:
- filiform loop, in which the current density is constant
- there are no nonlinear magnetic materials in the domain of magnetic field generated by the current closed loop
Principle
We consider the simple example of a rectangular loop of current, where C = S1∪S2∪S3∪S4.
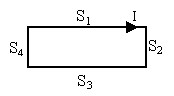
The line integral of the vector potential A on contour C can be split up into each of the four segments of the rectangular loop:
![]()
In the same way, the vector potential at any point can be seen as the sum of the contribution of each segment of the rectangular loop:
![]()
Thus, the inductance of the loop can be expressed by the following double sum:
![]()
where ![]() is the vector
potential created by the loop segment Sn.
is the vector
potential created by the loop segment Sn.
Partial inductance: definition
The inductance of the previously calculated loop can also be expressed by the following double sum:
![]()
where MPmn represents the partial inductance between the loop segments Sm and Sn.
![]()
For m ≠ n, it is about a partial mutual inductance MP
For m = n, it is about a partial self-inductance LP
Analytical formulas can be developed for parallelepiped-shaped portions of parallel conductors; they are given in section Analytical formulas.
When these portions (or PEEC elements) are positioned at an angle, numerical integration techniques must be used to calculate the partial mutual inductance. More details are given in section Semi-analytical formulas.
On the other hand, the mutual inductance between two perpendicular conductors is null.
Generalization
This formulation is not limited to the case of an isolated loop. It can be extended to more complex systems.
By splitting up such a system into elementary segments, we obtain a square, symmetric matrix of inductances, in which the diagonal terms correspond to partial self-inductances, and the non-diagonal terms correspond to partial mutual inductances.