Real case: volume conductors
Introduction
This paragraph gives the analytical expression of partial inductance in the real case of two volume parallel conductors (of non-negligible cross-section area). This expression is deduced from the previous expression by successive integrations on the width and thickness of each conductor.
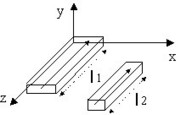
Reminder: The partial inductance between segments S1 and S2 is expressed by the formula:
![]()
Computation hypotheses
The computation hypotheses are the following:
- the current density is uniform in the cross-section area of the conductors
- the conductors have a rectangular shape in the cross-section
Obtaining the formula
The final formula of partial inductance between volume conductors is obtained after four successive integrations as presented in the figure below.
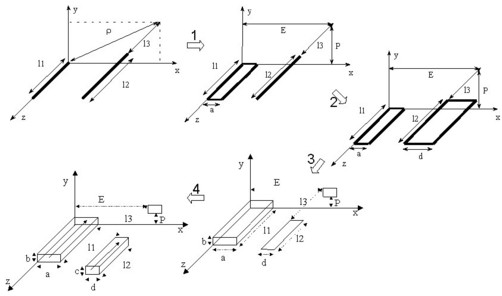
According to the geometric configuration of the two conductors, for example if they are very distant, it is possible to stop the integration at various levels in order to obtain a less complicated expression (integration over the width or integration on the thickness).
Partial inductance between two conductors
Under further examination is the study of partial inductance between two conductors in the configuration presented below.
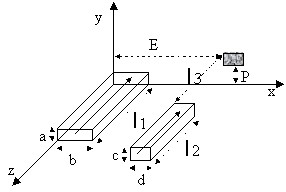
The analytical expression below gives the value of mutual inductance in µH if the distances are expressed in cm.
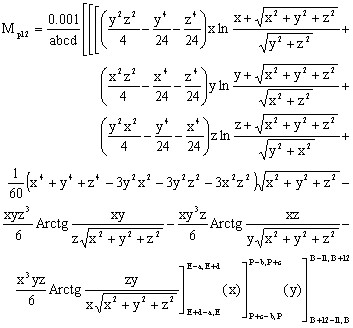
where:
![]()
Partial inductance of a conductor
The partial inductance of a volume conductor is a particular case. It is obtained by applying the previous formula with a = c, b = d, l1 = l2, l3 = 0, E = 0, P = 0.