SS-V：6000 简支薄方板 - 谐波强迫振动响应
测试编号 VD01 查看受谐波强迫振动的简支方板的瞬态响应。
定义
简支 10×10×0.05 m 的简支薄方板在均匀压力 P=100 Pa 的作用下，随时间呈如下函数变化。
其中，
- 激励频率。
激励频率的变化范围为从 0 至略高于方板的一阶共振频率。
采用十六 (16) 个模式来准确估算动力学解，所有模式均假定有 2% 的模态阻尼。
材料属性为：
- 属性
- 值
- 弹性模量
- 2.e+11 Pa
- 泊松比
- 0.3
- 密度
- 8.e+3 kg/m3
结果
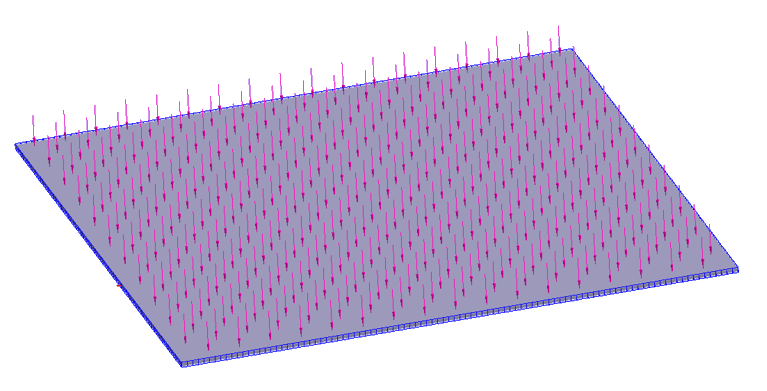
方板被模拟成一个 3D 实体。为了施加铰支座，在板的平面中间处创建了载荷线 (Figure 1)。 图 1.
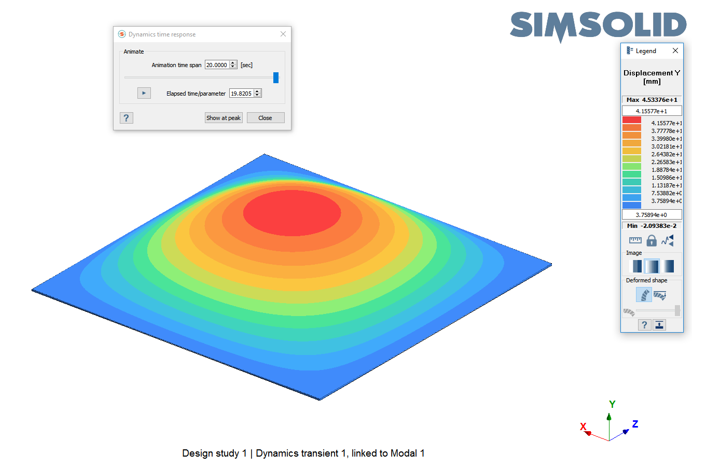
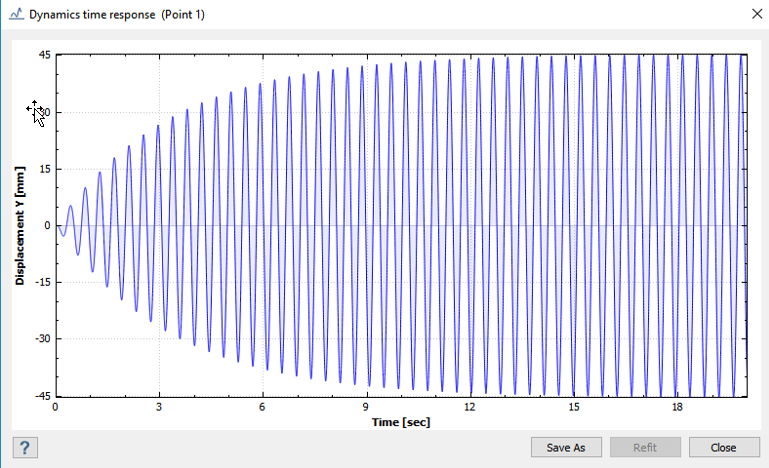
当激励频率等于方板的一阶固有频率时，响应达到峰值。它发生在激励开始后 19.82 秒。图 2.
下表列出了峰值响应比较。
| 偏移 Y，mm | 曲面应力，MPa | |
|---|---|---|
| 45.34 | 31.86 | SimSolid，实体模型 |
| 45.42 | 35.08 | 参考，薄方板 |
1 Test 13H from NAFEMS Publication R0016, “Selected Benchmarks for Forced Vibration”（强迫振动的选定基准） J. Maguire, D.J.Dawswell, L. Gould