MV-1080: Create an Analysis Using MDL
Tutorial Level: Intermediate In this tutorial, you will learn how to create an analysis definition and instantiate it in an MDL file.
An analysis definition is similar to a system definition in
syntax and usage except for these key differences:
- Analysis definitions use *DefineAnalysis(), while system definitions use *DefineSystem().
- Analysis can be instantiated under the top level Model only.
- Only one analysis can be active in the model at a given instance.
An analysis definition block begins with
*DefineAnalysis() and ends with
*EndDefine(). All entities defined within this block are
considered to be part of the analysis definition. The syntax of
*DefineAnalysis() is shown
below:
*DefineAnalysis(ana_def_name, arg_1,arg_2, ..., arg_n)ana_def_nameThe variable name of the analysis definition which will be used while instantiating the analysis.arg_1,arg_2...arg_nA list of arguments passed to the analysis definition as attachments.
Table 1
illustrates an analysis definition and its subsequent instantiation within an MDL
file. Two files, an analysis definition file and the model file, work together when
instantiating a particular analysis under study. Some of the terms in the example
are in bold to highlight a few key relationships between the files.
| Reference Numbers | System Instantiation with Definition |
|---|---|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
Table 2
details the relationships between the analysis definition and its instantiation in
the MDL Model file.
| Variable | Relationship |
|---|---|
j_joint_att |
The varname of the attachment, declared in the *Attachment() statement (line 4) in the analysis definition file, appears as an argument in the *DefineAnalysis() statement (line 3). A motion is applied on this joint using the *Motion() statement (line 6). |
ana_def |
The varname of the analysis definition is specified in the *DefineAnalysis() statement (line 3). The analysis definition is used by ana1 in the *Analysis() statement (line 2). |
Create the Analysis Definition File
In this step you will create the analysis definition file.
- Use the following function expression to create the impulse torque about the x
axis:
Tx = step(TIME,.3, 0, .31, 10) + step(TIME, .31, 0, .32, -10) - Apply this torque to estimate the natural frequencies of the triple pendulum
model shown in Figure 1:
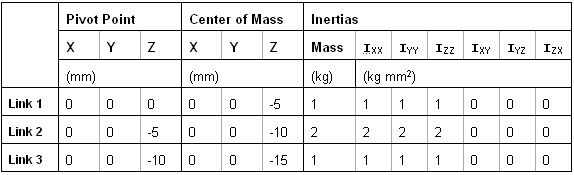
Figure 1. Schematic representation of a triple pendulum in stable equilibrium 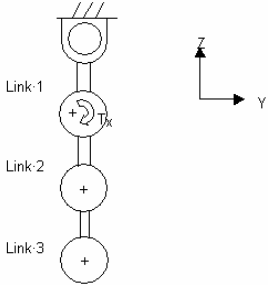
There are four MDL statements used in this
exercise:
*Attachment()
*ActionReactionForce()
*SetForce()
*Output() Note: Refer
to the MotionView Reference Guide
(located in the HyperWorks Desktop Reference Guide) for the syntax
of the above MDL statements.
- In a text editor, open an empty file.
- Create the *DefineAnalysis() and *EndDefine() block. You will add all other statements between this block.
-
In the text editor, define an analysis with a variable name of
def_ana_0and one argumentj_attas an attachment:*DefineAnalysis(def_ana_0, j_att) -
You can apply the torque between two bodies connected by a revolute joint, with
the origin of the joint taken as the point of application of the force. This
allows you to have only one attachment (the revolute joint). Create an
*Attachment() statement which defines
j_attas the attachment andJointas the entity type. Make sure that the variable name used in the statement is the same as is used in the *DefineAnalysis() statement.*Attachment(j_att, "Joint Attachment", Joint, "Select joint to apply torque")This allows you to only have one attachment; the revolute joint. -
Use the *ActionReactionForce() statement to define an
applied torque.
Remember: Reference the correct properties of the attachment joint to reach the bodies involved in the joint. Refer to the description of the dot separator in MDL. You can access properties of an entity by using the dot separator. For example, bodies attached to the revolute joint can be accessed as:
<joint variable name>.b1and as<joint variable name>.b2 -
Create a *SetForce() statement with a variable name of
force_1and the following torque values:TX = step(TIME,.3,0,.31,10) + step(TIME,.31,0,.32,-10),TY = 0,TZ = 0 -
Create an *Output() statement to output the applied
force.
-
Save the analysis situation as analysis.mdl.
The following shows what the file will look like:
*DefineAnalysis( def_ana_0,j_att ) *Attachment(j_att, "Joint Attachment", Joint, "Select joint to apply torque") *ActionReactionForce( force_1, "Torque", ROT, j_att.b1, j_att.b2, j_att.origin, Global_Frame ) *SetForce( force_1, EXPR, `step(TIME,.3,0,.31,10) + step(TIME,.31,0,.32,-10)`) *Output( o_force, "Input Torque", FORCE, FORCE, force_1, Global_Frame) *EndDefine()
Instantiate the Analysis in a Model
In this step, you will instantiate the analysis in the triple pendulum model.
- Lauch MotionView and open the triplependulum.mdl file from the mdl folder.
- From the Project Browser, click Model.
- In the Systems/Assembly panel, click the Import/Export tab.
-
Click the
 (file browser) and select
analysis.mdl. Then click
Import.
(file browser) and select
analysis.mdl. Then click
Import.
-
Verify that the Select a definition drop-down menu is set to
Analysis.
Figure 3. 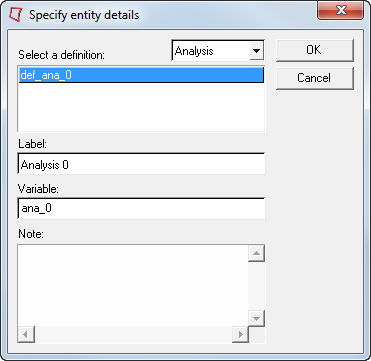
- Click OK.
- In the Project Browser, click the newly added Analysis 0.
-
Resolve the joint attachment.
- Save the model as new_triplependulum.mdl.
-
Run the model.
-
Click the
 (Run) panel
button.
(Run) panel
button.
- In the panel, specify an End time of 1.0 and a Print interval of 0.01.
- Click Run.
-
Click the
-
Use the
 (Start/Pause Animation) button
to view the animation.
(Start/Pause Animation) button
to view the animation.
- Use the .abf file from the solution to plot the "Input Torque" output.
