PBEAMC
Geometric Properties ElementPBEAMC lets you specify the geometric properties for an associated beam element of a circular cross section
Format
<PBEAMC
id = "integer"
mid = "integer"
ri1 = "real"
ro1 = "real"
ri2 = "real"
ro2 = "real"
nf = "real"
nx = "integer"
nr = "integer"
nt = "integer"
ngx = "integer"
ngr = "integer"
ngt = "integer"
graph = "integer"
/>Attributes
- id
- Unique beam property identification number.
- mid
- Material property identification number.
- ri1
- Inner radius of the element cross section at node (1).
- ro1
- Outer radius of the element cross section at node (1).
- ri2
- Inner radius of the element cross section at node (2).
- ro2
- Outer radius of the element cross section at node (2).
- nf
- Specify a number greater than or equal to zero. The value of this attribute is used to reduce the bending stiffness of this element.
- nx, nr, nt
- Number of integration points in X, radial and tangential directions.
- ngx, ngr, ngt
- Number of sub elements in X, radial and tangential directions. The default for ngx and ngr is 1, ngt is 10. 5.
- graph
- A post-processing flag that determines how this element is represented in the animation H3D. Default is 2.
Example
The example demonstrates the definition of a PBEAMC property element.
<PBEAMC id="61" mid="1" ri1="50.0" ro1="60.0" ri2="3.0" ro2="2.0" nx="5" nr="4" nt="10" />Comments
- This type of property card is used to specify the geometric properties of the BEAMC and BEAM9 element. Each beam property element must have a unique identification number.
- This property card defines the geometrical properties of the beam. The material properties of the beam are defined by the material specified by mid.
- If only ri1 and ro1 are specified, MotionSolve assumes the cross section of the beam to be constant. However, if additionally, ri2 and ro2 are specified, the radii are varied linearly from node 1 to node 2 to represent the beam in the animation H3D.
- For the beam element, nf can only be used with MAT6 to reduce the bending stiffness, that can related with the buckling stiffness.
- graph is a post processing flag that determines
how this element will be represented in the animation H3D file.
- graph = "0" implies that this element will not be represented in the H3D
- graph = "1" implies that this element will be represented as a line drawn between the two connecting nodes.
Figure 1. The representation of a circular beam with graph = 1. 
Note: When using graph="0" or graph="1", you will not be able to visualize the stress, strain or displacement contours. To do this, use graph="2" or graph="3".- graph = "2" implies that
the beam will be represented by 3D solid elements. This
mode is useful when trying to visualize the stress/strain
and displacement contours.
Figure 2. The representation of a circular beam with graph = 2. The beam is represented by 3D elements 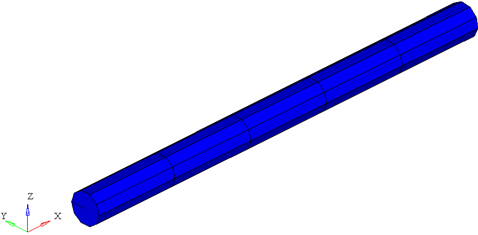
- graph = "3" implies that the beam is represented both as 3D solid elements as well as a line connecting the two nodes of the beam. This is useful when you need to visualize both the center line and the 3D representation of the beam.
Figure 3. The representation of a circular beam with graph = 3. The 3d elements in the middle of the beam are turned off to show the center line of the beam 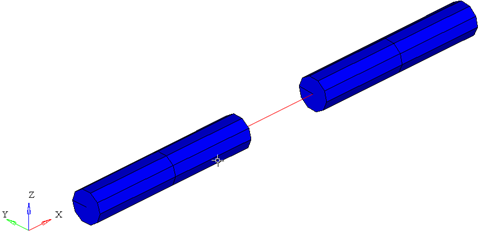
When representing the beam as a solid, the arguments ngx, ngr and ngt determine the number of elements that are used to represent the beam in the animation H3D.
Figure 4. Effect of ngx, ngr and ngt on the 3D representation of a simple circular beam 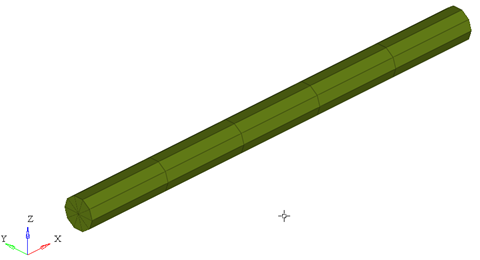
ngx = ngr = 1; ngt = 1
Figure 5. 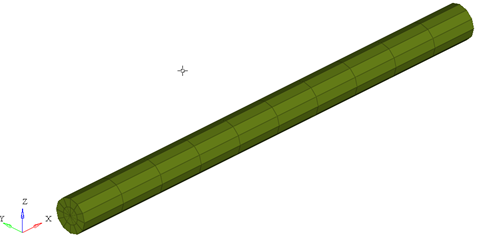
ngx = ngy = 2; ngt = 12
While increasing the ngx, ngr and ngt results in a better representation of the beam, it also increases the post-processing time taken by MotionSolve to write out the H3D. In addition, large values of ngx, ngr and ngt will increase the file size of the H3D considerably. Consider using the minimum values of these attributes that satisfy your visualization needs.