Linear Effects Post Processing

Measure the result of a single variable moving.

Analyze Linear Effects

Analyze the effects of input variables on output responses while ignoring the effects of other input variables in the Linear Effects post processing tab.

Linear effects are calculated using a linear regression model for the normalized input variable ranges of [-1, 1]. The linear effect value of input variable x on output response f(x, y) doubles the coefficient a1 of the regression model for f(x)=a0+a1*x. This term, A1, can be written compactly as cov(x,y)/var(x)*(x_max-x_min).

  1. From the Post Processing step, click the Linear Effects tab.
  2. Using the Channel selector, select the input variable(s) and output response(s) to analyze.
  3. Change the format to display linear effects by switching the view between (Linear Effects plot) and (Linear Effects Table).
    • In the Linear Effects Plot view, effects are represented by the slope of a line.
    • In the Linear Effects Table view, effects are presented in a tabular format.
  4. Analyze the linear effects.
Tip: Display selected data in a single plot or separate plots by switching the Multiplot option between (single plot) and (multiple plots).
Configure the linear effect table or plot display settings by clicking (located in the top, right corner of the work area). For more information about these settings, refer to Linear Effects Tab Settings.

Linear Effects Tab Settings

Settings to configure tables/plots displayed in the Linear Effects post processing tab.

Access settings from the menu that displays when you click (located above the Channel selector).
Normalize X-Axis
Scatter
Show scatter points in Linear Effects table.

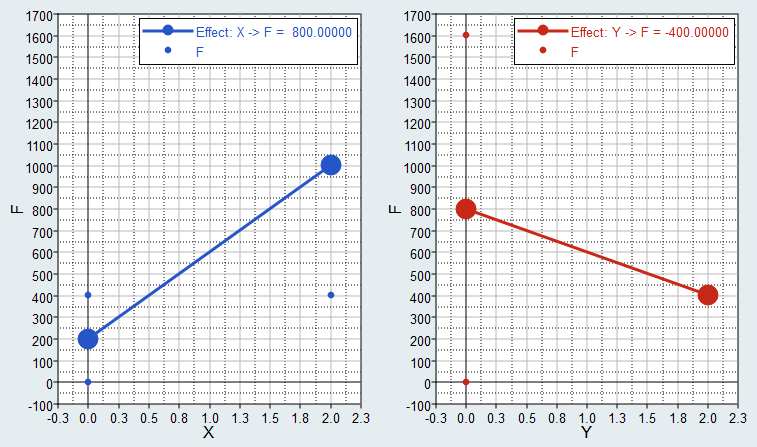
Example: Linear Effects

For two-level design of experiments, linear effect values can also be calculated as the difference between the average output responses when the input variable is at its lower value and when the input variable is at its upper value.

Given a two variable, two-level Full Factorial DOE matrix over the design space of [0:2] on both parameters as:
Table 1. Design Matrix
Run X Y F(X,Y)
1 0 0 1
2 0 2 401
3 2 0 1601
4 2 2 401
  • When X is at lower level, the mean output response is (1 + 401) / 2 = 201
  • When X is at upper level, the mean output response is (1601 +401) / 2 = 1001
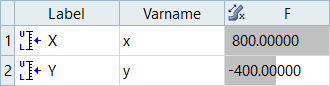
  • The effect of X on F is then (1001 - 201) = 800
  • When Y is at lower level, the mean output response is (1 + 1601) / 2 = 801
  • When Y is at upper level, the mean output response is (401 + 401) / 2 = 401
  • The effect of Y on F is then (401 - 801) = -400
Figure 1. Linear Effects Plot


Figure 2. Linear Effects Table


Note: HyperStudy calculates linear effects using a regression based on the data set. In this example, the regression is f(x) is ao+a1*x; where a1 is equal to 400.0 and x is between -1.0 and 1.0. The linear effect of the input variable x on the output response f(x,y) is 800.0.