Sine Sweep Fatigue Analysis

The study of fatigue life of structures under Sinusoidal Loading.

Frequency Response Stress results from the Frequency Response Analysis are used to calculate the frequency-dependent stress range, which are subsequently used to calculate Fatigue damage based on sweep rate.

Input

Sine sweep is a well-known method of vibration testing which is conducted to evaluate the vibration behavior of a specimen.

Fatigue analysis can be subsequently performed in sine sweep vibration to determine the fatigue life of the specimen. Sine sweep involves placing the specimen in a shaker and subjecting it to sinusoidal loading of varying amplitudes and frequencies of vibration, typically from low frequency, high amplitude, to high frequency, low amplitude or vice-versa.

Figure 1. Varying Amplitude Stress Data with Increasing Frequency

The following input information is required to characterize a sine sweep fatigue analysis:

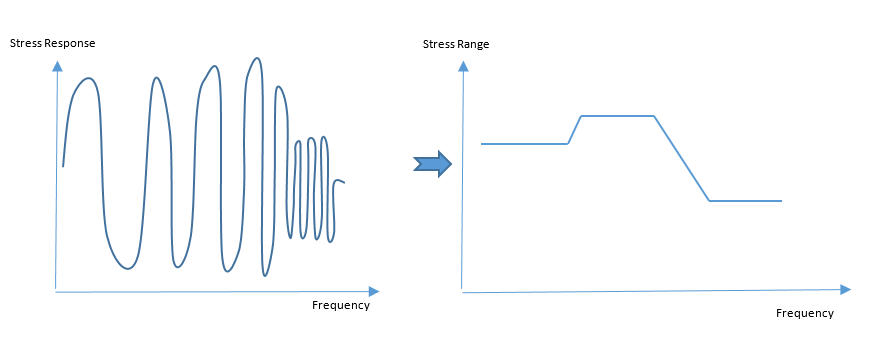
The Frequency Response subcase provides the input sinusoidal vibration profile that is required to conduct sine sweep fatigue analysis.
The corresponding sine sweep parameters, i.e. theSR (sweep rate) and SRUNIT (sweep rate unit) fields, are specified with each fatigue event created.
The frequencies at which the sine sweep fatigue calculation are performed are specified in SN or EN uniaxial contexts.
The static subcase can be added to the event in the load map for mean stress correction.
The number of sweeps are to be specified alongside the event (default = 1 Sweep). The number of sweeps will be considered as time ‘T’ seconds if only one Frequency is considered, or if the SR = 0.0.

Stress-Life

Uses the frequency-based stress range output from Frequency Response Analysis to compile a Damage versus Frequency curve.

The key for Sine Sweep Fatigue Analysis is to find the number of cycles that occur per frequency. Subsequently, the amount of Damage per cycle at a particular frequency can be calculated. This is multiplied by the number of cycles at that frequency to find the total damage per frequency. This is then integrated over the entire frequency range to find the damage per sweep. Fatigue damage for multiple sweeps is just a multiplication of the damage per sweep times the number of sweeps.

Sweep Rate in Hertz Per Second (SRUNIT=HZPS)

Sweep rate in Hertz per second implies the following relationship between frequency and time, for a given sweep rate $υ$ .

f = f_{0} + υ t

Where,

$f$: Frequency value of interest .
$f_{0}$: Initial frequency value of loading frequency range from Frequency Response subcase.
$υ$: Sweep rate in Hertz per second (SR field in the load map).
$t$: Time at which the stress range $Δ σ_{f}$ is applied with a frequency $f$ in sine-sweep fatigue.

The stress range versus frequency is output from the Frequency response analysis. This is used to identify the stress range for a particular frequency. To calculate the number of cycles of the stress range, $Δ σ_{f}$ , at a particular frequency, the following formula is used.

n_{f}^{c y c} = \frac{d n}{d f} = f \frac{d t}{d f} = f \frac{1}{υ}

Where,

$f$: Frequency value of interest .
$υ$: Sweep rate in Hertz per second (SR field in the load map).

Note: The Sweep rate is defined in Hertz per second.

You can see that the number of cycles of a stress range $Δ σ_{f}$ at a particular frequency $f$ is equal to $n_{f}^{c y c}$ . This can be also defined as the rate of change of number of cycles with respect to frequency, at an arbitrary frequency.

The damage value per cycle $D^{c y c} (f)$ at frequency $f$ , is calculated based on the stress range $Δ σ_{f}$ from the SN curve.

D^{c y c} (f) = D_{S N}^{Δ σ_{f}}

Where,

$D^{c y c} (f)$: Damage per cycle at frequency $f$
$D_{S N}^{Δ σ_{f}}$: Damage value corresponding to stress range $Δ σ_{f}$ from the SN curve.

Figure 2. Damage versus Frequency: Area Under this Curve is the Total Damage Per Sweep

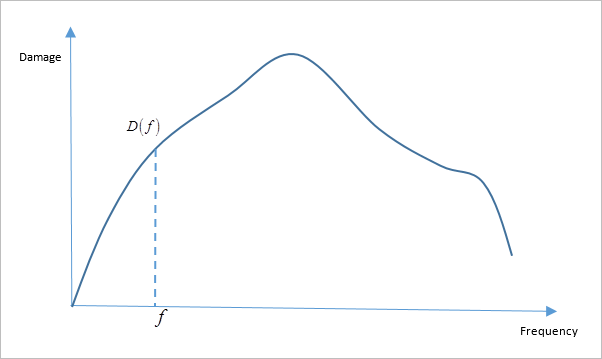
Based on the damage per cycle at a frequency, $D^{c y c} (f)$ , a curve of Damage versus Frequency is constructed. This is constructed by first calculating the Damage per frequency:

D (f) = D^{c y c} (f) * n_{f}^{c y c}

Where, $D (f)$ is the damage per frequency.

Based on the Miner’s Damage accumulation rule, the total damage for a single sine sweep is calculated by integrating for the area under the Damage versus frequency curve.

D_{S w e e p} = \int D (f) d f

Where, $D_{S w e e p}$ is the total damage per sweep.

The total damage is calculated by multiplying the damage for each sweep by the number of sweeps.

D_{T o t a l} = N_{S w e e p s} * D_{S w e e p}

Where, $N_{S w e e p}$ is the number of sweeps.

If SR=0.0 (no sweep) or only one loading frequency is defined in the frequency response subcase, then the damage value is calculated for that particular frequency. In the case of SR=0.0, the first loading frequency in the frequency response subcase is used. For the case of a single loading frequency input on frequency response subcase, that particular frequency is chosen. In such cases, the total damage is the damage per frequency multiplied by the total time T# defined for the event.

Sweep Rate in Octaves Per Minute (SRUNIT=OCTPM)

If the Sweep rate is defined in Octaves per minute, the sweep rate calculation involves a different equation compared to that of Hertz per second.

Sweep rate in Octaves per minute implies the following relationship between frequency and time, for a given sweep rate $υ$ .

f = f_{0} * 2^{υ t}

Where,

$f$: Frequency value of interest .
$f_{0}$: Initial frequency value of loading frequency range from Frequency Response subcase.
$υ$: Sweep rate in Octvates per minute (SR field in the load map).
$t$: Time at which the stress range $Δ σ_{f}$ is applied with a frequency $f$ in sine-sweep fatigue.

Applying natural logarithm function on both sides and taking derivative with respect to frequency, the equation reduces to:

\frac{d t}{d f} = \frac{1}{\ln 2} * \frac{1}{υ} * \frac{1}{f}

n_{f}^{c y c} = \frac{d n}{d f} = f \frac{d t}{d f} = f * \frac{1}{\ln 2} * \frac{1}{υ} * \frac{1}{f} = \frac{1}{υ \ln 2}

Where,

$f$: Frequency value of interest .
$υ$: Sweep rate in Octvates per minute (SR field in the load map).

Note: The Sweep rate is defined in Octaves per minute.

You can see that the number of cycles of a stress range $Δ σ_{f}$ at a particular frequency $f$ is equal to $n_{f}^{c y c}$ (which can also be defined as the number of cycles per unit frequency, at an arbitrary frequency). Also, from the formula, for the case of Octaves per minute, the number of cycles of each frequency is independent of the frequency. Therefore, all frequencies have the same number of cycles.

The damage value per cycle $D^{c y c} (f)$ at frequency $f$ , is calculated based on the stress range $Δ σ_{f}$ from the SN curve.

D^{c y c} (f) = D_{S N}^{Δ σ_{f}}

Where,

$D^{c y c} (f)$: Damage per cycle at frequency $f$
$D_{S N}^{Δ σ_{f}}$: Damage value corresponding to stress range $Δ σ_{f}$ from the SN curve.

Based on the damage per cycle at a frequency, $D^{c y c} (f)$ , a curve of Damage versus Frequency is constructed (Figure 2). This is constructed by first calculating the Damage per frequency.

D (f) = D^{c y c} (f) * n_{f}^{c y c}

Where, $D (f)$ is the damage per frequency.

Based on the Miner’s Damage accumulation rule, the total damage for a single sine sweep is calculated by integrating for the area under the Damage versus frequency curve.

D_{S w e e p} = \int D (f) d f

Where, $D_{S w e e p}$ is the total damage per sweep.

The total damage is calculated by multiplying the damage for each sweep by the number of sweeps.

D_{T o t a l} = N_{S w e e p s} * D_{S w e e p}

Where, $N_{S w e e p}$ is the number of sweeps.

Strain-Life

Used for vibration based fatigue is calculated based on the damage caused by the highest stress-range.

The process for Strain-life fatigue is similar to that of stress-life, wherein, the characterization of number of cycles versus the stress-range is utilized to calculate the damage due to sine-sweep.

Since loading and unloading path information is lost in vibration analysis, the strain-life approach in vibration fatigue is a conservative extension of the stress-range based data.

Strain-life fatigue analysis is typically conducted for situations where plastic strain is encountered. In such cases, the greatest energy loss (largest stress-strain hysteresis loop) occurs for the cycle with largest strain range. Since this is the largest strain range, the damage is also the highest for this one cycle compared to the rest of the lower strain-range cycles. First, Neuber correction is applied to convert Stress-Range data to Strain-Range data.

Figure 3. Neuber Correction: Histogram Bar Graph for Cycles versus Stress Range Converted to Cycles versus Strain Range

Based on Figure 3, you can see that the stress range SR3 leads to the ER3 Strain range which leads to maximum damage and also the largest stress-strain hysteresis loop. All other stress-strain hysteresis curves will lie inside this curve, since they will cause lower damage and have lower strain energy loss compared to the highest cycle.

Figure 4. Strain-Range Histogram Illustrated as Stress-Strain Hysteresis Loops

Note: Zero mean stress is considered for EN Sine sweep fatigue. Therefore, the stress-strain curves are symmetric about the stress and strain axes for all strain ranges.

For strain-life sine sweep fatigue, the strain ranges for each of the inner hysteresis loops are based on corresponding stress range values at which the loading was applied. These loops are now pushed upward until the top of the loops touch the largest loop (this process is known as hanging). Similarly, this process is repeated for all inner loops until all loops touch the corresponding topmost point of the largest hysteresis loop.

Figure 5. Hanging Lower Strain-Range Hysteresis Loops to the Largest Hysteresis Loop

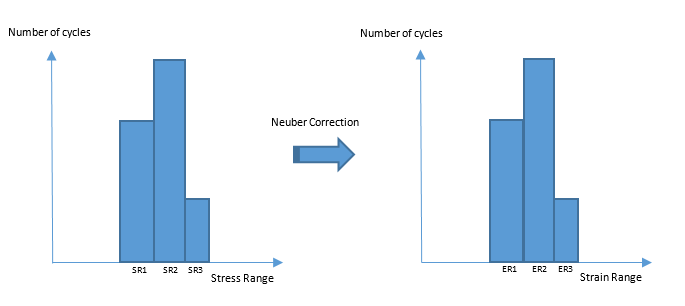
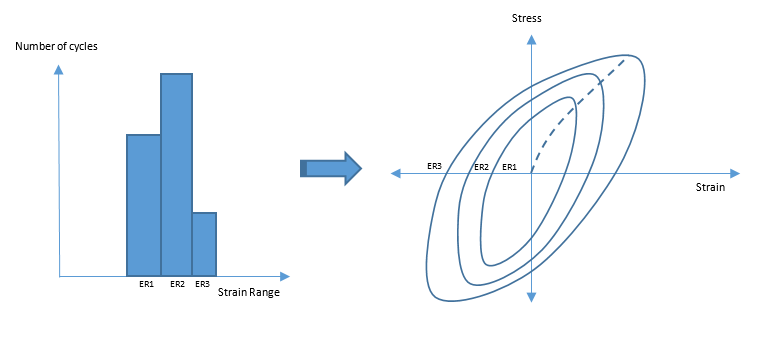
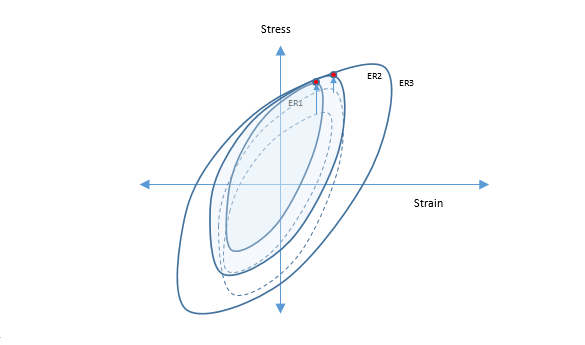
Using this updated stress strain cycle data, the rest of the sine-sweep procedure continues in the same way as in stress-life sine sweep fatigue analysis.

The number of cycles per frequency

n_{f}^{c y c}

, are calculated in the same way as in Stress-Life Sine Sweep Fatigue.

Note: The calculation is different for the case of Sweep rate in Hertz per second or Octaves per minute.

The SWT or Morrow damage models are used to incorporate the effect of updated stress information (as a result of hanging procedure explained in the previous section). The updated mean stress for the new inner loops is used for Morrow and the updated maximum stress for the new inner loops is used for SWT damage models.

The damage value per cycle $D^{c y c} (f)$ at frequency $f$ , is calculated based on the strain values and updated mean/maximum stress range from the EN curve. For further information, refer to Mean Stress Correction.

D^{c y c} (f) = D_{E N}^{Δ ε_{f}}

Where,

$D^{c y c} (f)$: Damage per cycle at frequency $f$
$D_{E N}^{Δ σ_{f}}$: Damage value corresponding to strain and updated mean stress from the EN curve.

Based on the damage per cycle at a frequency, $D^{c y c} (f)$ , a curve of Damage versus Frequency is constructed (Figure 2). This is constructed by first calculating the Damage per frequency.

D (f) = D^{c y c} (f) * n_{f}^{c y c}

Where,

$D (f)$: Damage per frequency.

Based on the Miner’s damage accumulation rule, the total damage for a single sine sweep is calculated by integrating for the area under the Damage versus Frequency curve.

D_{S w e e p} = \int D (f) d f

Where,

$D_{S w e e p}$: Total damage per sweep.

Current Support of Sine Sweep Fatigue Analysis

Only von Mises is supported for the stress combination.
Only uniaxial fatigue analysis is supported.
SN and EN for solid and shell elements are supported.
Only one FRF subcase is allowed per sine sweep event.