Transformation : à propos

Utilisation

Les transformations sont des fonctions géométriques qui facilitent la construction par propagation ou par extrusion de nouvelles entités géométriques sur la base d'entités déjà créées.

Fonctions

Les différentes fonctions disponibles sont :

  • la translation
  • la rotation
  • l'affinité (ou homothétie), y comprise donc la symétrie
  • la transformation composée

Translation

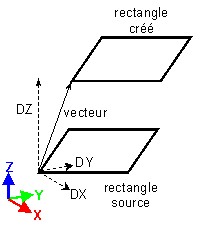
Une translation est définie par une direction et une distance.

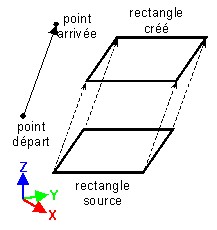
Translation définie par un vecteur Translation définie par deux points et un rapport
  • la direction et la distance sont fixées par :
    • un repère de travail
    • un vecteur (ses composantes DX, DY et DZ fixent la direction et l'amplitude du vecteur)
  • la direction est fixée par les deux points (point départ et point arrivée)
  • la distance est égale à la distance entre les deux points (point départ et point arrivée) multipliée par le rapport (coefficient de proportionnalité)

Rotation

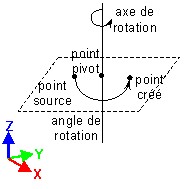
Une rotation est définie par un axe de rotation et un angle.

Rotation définie par trois angles et un point pivot
  • l'axe de rotation et l'angle sont définis par :
    • un repère de travail
    • un point pivot
    • et trois angles autour des axes X, Y et Z

Affinité / Homothétie

Cette transformation est définie par un rapport à un point, à une ligne ou à un plan. On parle d'homothétie si elle est définie par rapport à un point et d'affinité dans les autres cas.

Le résultat d'application de cette transformation dépend du rapport d'affinité (cf. tableau ci-dessous).

Rapport Résultat
k = -1 symétrie
k = 1 identité
k = 0 projection
k > 1 agrandissement (affinité / homothétie agrandissante)
0 < k < 1 réduction (affinité / homothétie réductrice)
k < -1 agrandissement (affinité / homothétie agrandissante négative)
-1 < k < 0 réduction (affinité / homothétie réductrice négative)
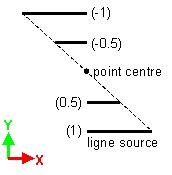
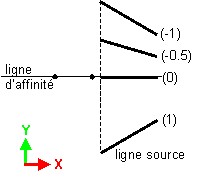
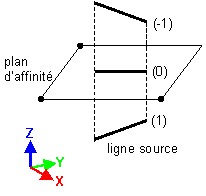
Homothétie par rapport à un point Affinité par rapport à une droite Affinité par rapport à un plan
Avertissement : Le rapport d'affinité k = 0 provoque une erreur dans l'application de l'affinité par rapport à un point, car l'entité géométrique en question (point, ligne, face ou volume) est déjà existante (dans le cas d'un point) ou dégénérée et réduite à un point (dans les cas d'une ligne, d'une face ou d'un volume).

Symétrie

Une symétrie est un cas particulier (k = -1) d'affinité (voir ci-dessus) ; elle est donc définie par un rapport à un point, à une ligne ou à un plan.

Composition de transformations

Il est possible de créer des transformations géométriques composées de deux transformations déjà existantes.

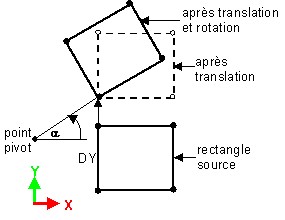
Transformation composée de deux transformations :

  • une translation suivant l'axe OY (définie par DX = 0, et DY)
  • une rotation autour de l'axe Z (définie par un point pivot et un angle α)
Avertissement : En utilisant l'ordre inverse de deux transformations on n'obtient pas le même résultat.

Paramétrage

Les caractéristiques de définition des transformations sont des grandeurs paramétrables. Les composantes de vecteur, les coordonnées de point pivot, les angles de rotation et le rapport d'affinité peuvent être définis à l'aide d'une expression algébrique.

Une expression algébrique peut contenir :

  • des constantes
  • des paramètres géométriques (préalablement créés)
  • les fonctions mathématiques de base utilisant des opérateurs : +, -, *, /, ( )
  • les fonctions mathématiques usuelles admises par le FORTRAN

Les fonctions mathématiques sont décrites dans la section Fonctions.