Electrique transitoire: équations résolues

Introduction

Dans une application Électrique transitoire, les équations utilisées pour la résolution sont :

• les équations de Maxwell (pour un système électrique)
• les équations constitutives de la matière, caractérisant les milieux diélectriques

Les conditions de calcul pour une application Électrique transitoire sont les suivantes :

• l'étude est une étude temporelle : d/dt ≠ 0
• on s'intéresse aux champs D et E (les champs B et H ne sont pas calculés)

Les équations en champs électriques E, D et en champs magnétiques B, H sont découplées

Équations et conditions

Dans les conditions de calcul énoncées précédemment, les équations se résument de la façon suivante :

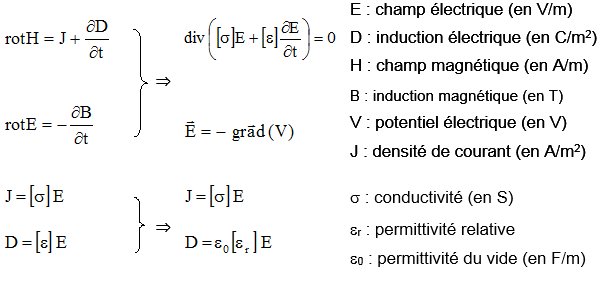
Rappel sur les opérateurs différentiels : La divergence du rotationnel d'un champ est toujours nulle : div (rot (Champ)) = 0

Équation résolue

L'équation résolue par la méthode des éléments finis dans une application Électrique transitoire est l'équation suivante:

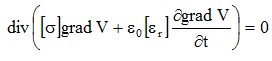
où:

• [σ] est le tenseur de conductivité du milieu (en S)
• [εr] est le tenseur de permittivité relative du milieu
• ε₀ est la permittivité du vide ; ε₀ = 1/(36 π 10⁹) (en F/m)
• V est le potentiel électrique (en V)

Variable d'état

La variable d'état est le potentiel électrique V (noté Ve dans Flux 3D).

Pour que le potentiel V soit entièrement défini, il faut imposer ce potentiel au moins en un point.