ifft
Inverse Fast Fourier transform.
Syntax
x = ifft(f)
x = ifft(f,n)
x = ifft(f,n,dim)
Inputs
- f
- The frequency spectrum to be transformed into the time domain.
- n
- Size of the ifft.
- dim
- The dimension on which to operate.
Outputs
- x
- The time domain representation of f.
Example
ifft of signal with two frequency components.
The example shows how to generate a time domain signal from its frequency domain input. The input is sparse, so the example then shows how to up-sample the result to produce a densely sampled signal.
ft = [0 0 0 0 0 -10i 0 0 6i 0 0 0 -6i 0 0 10i 0 0 0 0]; % frequency domain input
fs = 100; % sampling frequency
n = 20; % number of samples
ts = 1/fs; % sampling time interval
time = [0:ts:(n-1)*ts]; % time vector
signal = ifft(ft); % time signal
plot(time, signal);
hold on;
nn = 200; % new number of samples
newtime = [0:ts:(nn-1)*ts]*(n/nn); % new time vector
newsig = ifft(ft,nn); % new time signal
plot(newtime, newsig);
legend('sparse signal','dense signal');
xlabel('time');
ylabel('amplitude');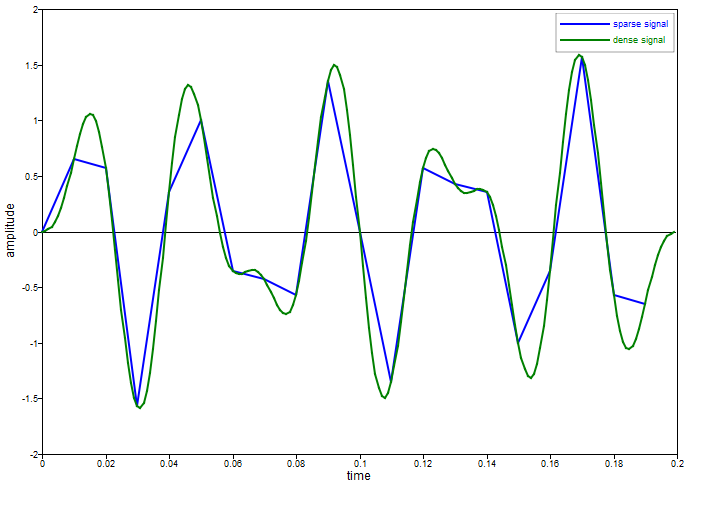
Figure 1. fft figure 1
The frequency spacing is fs/n = 5 Hz, so both components fall exactly on one of the frequency vector values.
Comments
The ifft is applied to a vector input, or to each column vector of a matrix input. The n times associated with the outputs are spaced in increments of 1/fs, where fs is the sampling frequency. The times span from 0 to (n-1)*ts. A common use of ifft is to regenerate a time domain signal following the application of a frequency domain filter after an fft. The size of the fft, n, defaults to the length of the vector being transformed. If n is not the default, the spectrum vector is either truncated or extended with zeros symmetrically with respect to the Nyquist frequency. The effect on the time domain is to insert additional samples in the sampling time span. Raising the value of n beyond the default value effectively increases the Nyquist frequency while retaining all of the frequency content. The effect is that the original signal from which the input spectrum was created is upsampled. In a similar way, decreasing n effectively downsamples the original signal. ifft uses the FFTW library.