CONGM
Concentrated Mass ElementCONGM defines a concentrated mass element at an NLFE grid.
Format
<CONGM
id = "integer"
gid = "integer"
mass = "real"
[
x = "real"
y = "real"
z = "real"
]
i11 = "real"
i22 = "real"
i33 = "real"
[
i21 = "real"
i31 = "real"
i32 = "real"
]/>Attributes
- id
- Unique identification number.
- gid
- Grid identification number.
- mass
- First grid identification number.
- xyz
- X, Y and Z offset distance from the grid point to the center of gravity. Default for x, y and z is 0.
- i11
- i22
- i33
- Mass product of inertia about X, Y and Z axes respectively.
- i21
- i32
- i33
- Mass product of inertia about X-Y, X-Z and X-Y respectively. Default value for all three attributes is 0.
Example
The example demonstrates the definition of a CONGM element.
<CONGM id="1" gid="17" mass="10" i11="1" i22="1" i33="1"/>Comments
- The x, y and z coordinates of the mass center of gravity are represented in the global coordinate system.
- The form of the inertia matrix about its center of gravity is
calculated as:
Figure 1. 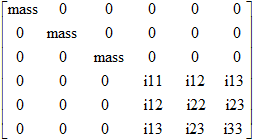
where,
and,
- All four grids defined for this element must be unique.