Home
Learn the Approaches
Each approach in HyperStudy serves a different purpose in the design study.
Optimization
An Optimization is a mathematical procedure used to determine the best design for a set of given constraints, by changing the input variables in an automatic manner.
Criteria for Formulating an Optimization Problem
In order to formulate a design problem as an optimization problem you must identify input variables, objective functions, and constraint functions.

Welcome
What's New
View new features for HyperStudy 2024.1.
Get Started
Learn the basics and discover the workspace.
Tutorials
Discover HyperStudy functionality with interactive tutorials.
Manage Files and Data
Create, open, import, and save models.
Perform Studies
A study is a self-contained project in which models, variables, output responses, and approaches are defined.
Learn the Approaches
Each approach in HyperStudy serves a different purpose in the design study.
- DOE
  A DOE is a series of tests in which purposeful changes are made to the input variables to investigate their effect upon the output responses and to get an understanding of the global behavior of a design problem. By running a DOE, you can determine which factors are most influential on an output response.
- Fit (Approximation)
  A Fit is a mathematical model that is trained by data and is capable of predicting output response variables for a given set of input variables.
- Optimization
  An Optimization is a mathematical procedure used to determine the best design for a set of given constraints, by changing the input variables in an automatic manner.
  - Criteria for Formulating an Optimization Problem
    In order to formulate a design problem as an optimization problem you must identify input variables, objective functions, and constraint functions.
  - Optimization Method Classification
    Optimization methods can be categorized, with respect to their search technique, as iterative or exploratory. Iterative techniques can be either a local or global approximation.
  - Optimization Methods
    Numerical methods available for an Optimization approach.
- Sampling Fit
  A Sampling Fit is a combination of space-filling DOE method and mathematical model trained by the data generated.
- Stochastic
  A Stochastic approach is a method of probabilistic analysis where the input variables are defined by a probability distribution, and consequently the corresponding output responses are not a single deterministic value, but a distribution.
- Basic
  A Basic approach can be used to test nominal values and bounds by performing a nominal run, system bound check, or sweep.
- Verification
  A Verification approach compares two data sets in a side by side comparison.
- PhysicsAI
  A PhysicsAI approach is used to build fast predictive models from simulation data.
Customize HyperStudy
Customize HyperStudy by registering solver scripts, functions, and optimizers, and defining user preferences files.
Keyboard Shortcuts
Keyboard shortcuts used to access HyperStudy features.
Frequently Asked Questions
This section provides quick responses to typical and frequently asked questions regarding HyperStudy.

View All Altair HyperWorks Help

Criteria for Formulating an Optimization Problem

In order to formulate a design problem as an optimization problem you must identify input variables, objective functions, and constraint functions.

When you put input variables, objectives and constraints together, you get the optimization formulation for a design problem as shown in Table 1.

Refer to Objectives and Constraints for more information.

Table 1.
Type	Formula(s)	Example
Objectives	$\min f (x)$	$\min cost ($)$
Constraints	$g (x) \leq 0.0$ $h (x) = 0.0$	$σ < σ a l l o w a b l e$
Design Space	$l o w e r x i \leq x i \leq u p p e r x i$ $2.5 m m < t h i c k n e s s < 5.0 m m$	$number of bolts \in (20, 22, 24, 26, 28, 30)$

Where:

$f (x)$ is the vector of system output responses that are used as objectives.
$g (x)$ and $h (x)$ is the vector or system output responses that are used as inequality and equality constraints.
$x$ is the vector of input variables.

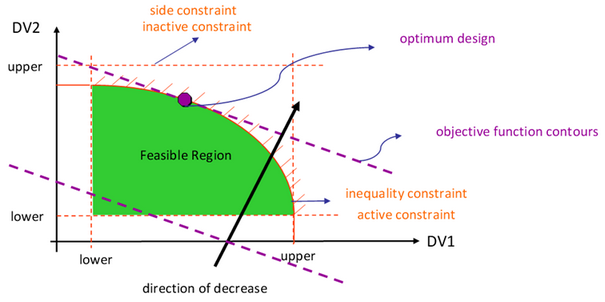
Some of the results that would be reported after an optimization run include but not limited to:

Optimum Design: The point or design that minimized (maximized) the objective function and at the same time satisfy all the constraints.
Violated Constraint: Constraint that is not satisfied.
Active Constraint: Constraint that is satisfied exactly; equality constraints are active for feasible designs.
Inactive Constraint: Constraint that satisfied but not on the bound.
Feasible Design: A point or a design that satisfies all the constraints.
Infeasible Design: A design that violates one or more constraints.

Figure 1. Design Space Definitions