Confounding and Resolutions
Confounding occurs when two factors are associated with each other or “travel together” and the effect of one is confused with the effect of the other.
Confounding
Resolution describes the degree to which estimated main effects are confounded with estimated 2-level interactions, 3-level interactions, and so on. For example, in order to improve team performance, a soccer coach asks his team to run two miles a day while the players decide to take vitamins. In this case the effects of running two miles a day and taking vitamins will be confounded since it will not be possible to identify the effect of them on team performance independently.
Confounding occurs whenever a Fractional Factorial design is chosen instead of a Full Factorial design. The consequence of confounding in DOEs is that the values calculated for main effects will have error coming from inclusion of higher order interactions in the calculation and interaction effects will be unknown. However Fractional Factorials also cost a fraction of the Full Factorial designs and therefore in the trade-off between cost and accuracy, they are preferred.
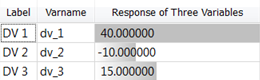
| DV 1 | DV 2 | DV 3 | output response of 3 input variables 200 + 3 * dv1 - 12 * dv2 + 8 * dv3 + 2 * dv1 * dv2 - dv1 * dv3 |
|
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 200 |
| 2 | 0 | 0 | 10 | 280 |
| 3 | 0 | 10 | 0 | 80 |
| 4 | 0 | 10 | 10 | 160 |
| 5 | 10 | 0 | 0 | 230 |
| 6 | 10 | 0 | 10 | 210 |
| 7 | 10 | 10 | 0 | 310 |
| 8 | 10 | 10 | 10 | 290 |
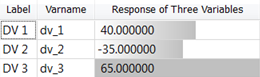
| DV 1 | DV 2 | DV 3 | output response of 3 input variables 200 + 3 * dv1 - 12 * dv2 + 8 * dv3 + 2 * dv1 * dv2 - dv1 * dv3 |
|
|---|---|---|---|---|
| 1 | 0 | 0 | 10 | 280 |
| 2 | 10 | 0 | 0 | 80 |
| 3 | 0 | 10 | 0 | 230 |
| 4 | 10 | 10 | 10 | 290 |
Resolution
Resolution describes the degree to which estimated main effects are confounded with estimated 2-level interactions, 3-level interactions, and so on. The design resolution tells us how badly the design is confounded. Resolution III designs confound main effects with two-factor interactions. Resolution IV designs confound main effects with three-factor interactions (A+BCD), as well as two-factor interactions with other two-factor interactions (AB+CD). Resolution V designs confound main effects with four-factor interactions, or two-factor interactions with three-factor interactions.
Higher resolution designs have less severe confounding, but require more runs. A resolution IV design is better than a resolution III design because we have less-severe confounding pattern in the `IV' than in the `III' situation. However in most cases higher-order interactions are less significant than low-order interactions and therefore there is not much benefit to higher resolution designs that come at the cost of additional computational expense.