RD-V: 0530 Wave Propagation
A sinusoidal imposed displacement is applied to a hollow sphere to study wave propagation.
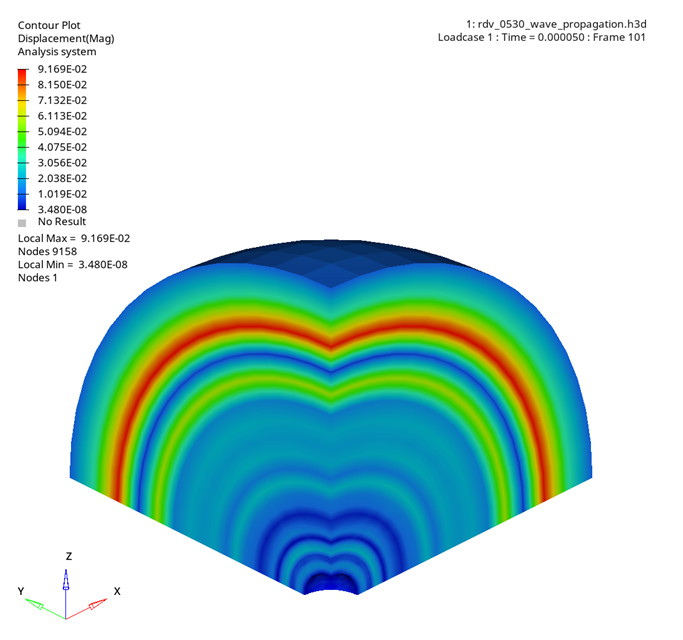
Wave propagation is studied by applying a sinusoidal imposed displacement to the inside of a hollow sphere. The max displacement of an inner and outer node is used to calculate the speed of sound in the material.
Options and Keywords Used
- Pressure load (/IMPDISP)
- Lagrange property formulation with Iale = 0 (default)
- Wave propagation in a solid material
Input Files
Model Description
Units: mm, s, Mg
A hollow sphere with an inner radius of 25.4 mm and an outer radius of 254 mm is modeled using 1/8th symmetry. The sphere was hex mapped meshed from the inside to the outside. To simulate symmetry, the x, y, and z faces are constrained in their respective directions. A radial sinusoidal imposed displacement is applied to the inner nodes of the sphere. The sine wave period is 1.0E-5 s with an amplitude of 1 mm. After 1.0E-5 seconds, the displacement is fixed at zero. The end simulation time is 5.0E-5 s. Local /SKEW coordinate systems are used to define the radial direction of the imposed displacement. Steel material properties are used in the model. Due to the short time duration of the simulation, the /DTIX option is used to define a smaller timestep, which results in more simulation cycles. For better accuracy, the function that represents the sine curve is defined with 1002 points.
Results
The analytical solution for the speed of sound in a material is calculated using the following formula. 1
- Modulus of elasticity
- Density
- Poisson's ratio
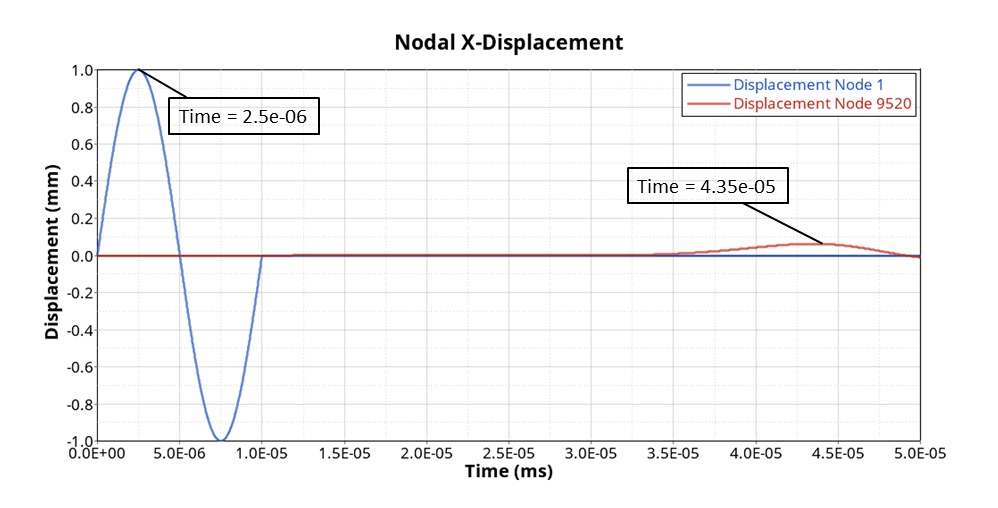
The calculated velocity from the simulation is 5.582 km/s compared to the analytical result of 5.79 km/s. This results in a numerical error of 3.59%.
Conclusion
The numerical error calculated for the speed of sound is small and could be reduced further by refining the mesh.