RD-V: 0110 Friction
The contact friction forces are studied and compared to an analytical solution.
Figure 1.
The contact friction forces are studied between a fixed and moving plate. The friction and reaction forces are used to calculate a displacement which is compared to the applied displacement.
Options and Keywords Used
- /INTER/TYPE24
Input Files
Model Description
| Total Displacement | ||
|---|---|---|
| 565 mm/s | 0.009 s | Y=2.54 mm |
| -102 mm/s | 0.001 s | Z=0.0508 mm |
The following system is used: mm, s, Mg.
Simulation Iterations
The contact reaction force was output to the time history file. The reaction force from the imposed velocity applied to the top block’s positive y face were also output to the time history file. The surface to surface /INTER/TYPE24 contact interface was studied.
Results
- Theoretical displacement in the y direction
- Length of the top block
- Width of the top block
- Height of the top block
- Young's modulus
- Total resultant force at the imposed velocity, calculated from /ANIM/VECT/FREAC
- Total contact reaction forces in the z direction from /TH/INTER
- Coefficient of friction
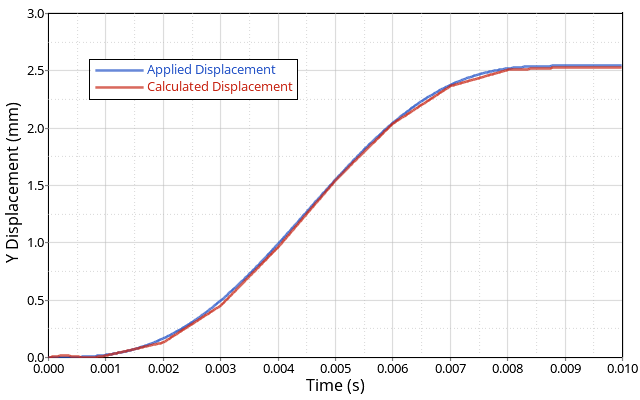
Figure 2. Applied Displacement and the Displacement Calculated
The calculated displacement, where the imposed velocity was applied in the y direction was 2.530 mm. When compared to the applied 2.540 mm displacement, there was a numerical error of 0.39%.
Conclusion
The contact interface friction calculation results in minimum error of 0.39% when compared to theory.