Surface Tension - Single Phase and Adhesion

Both single phase surface tension and adhesion modeling is based on the work of Akinci et al.

Both models are capable of reproducing qualitatively realistic results, but are in principle unphysical and cannot be generalized for an arbitrary case/simulation. Because of this, trial-and-error tuning of the surface tension coefficient and the adhesion coefficient is necessary if realistic fluid behavior is to be achieved.

Both adhesion and single phase surface tension models rely on a form inter-particle force, which binds the particles together. The way the force is modeled is through a specific kernel shape which mimics a potential energy well. In that sense, particles tend to keep a certain distance from each other and introduce elastic forcing if the particles get too close or too far from each other.

The equation that dictates the adhesion force is given by:(1)

F_{a d} = - \sum_{n b r s} β m_{i} W_{A k} V_{i} \frac{Δ x_{i j}}{| Δ x_{i j} |}

While the single phase surface tension is defined by:(2)

F_{c o h} = - \sum_{n b r s} \frac{2 ρ_{0}}{ρ_{i} + ρ_{j}} γ m_{i}^{2} W_{C o h} \frac{Δ x_{i j}}{| Δ x_{i j} |}

Where,

Indicies $A d$ and $C o h$ stand for adhesion and cohesion.

$W$ is the appropriate kernel used for each of the forces.

$m$ is the mass of the particle.

$Δ x_{i j}$ is the distance between two interacting particles.

$ρ_{i}$ and $ρ_{j}$ are instantaneous particle densities.

$ρ_{o}$ is the default density value of the particle phase.

$β$ is the adhesion coefficient.

$γ$ is the cohesion or surface tension coefficient.

The

β

parameter is specified for each WALL or MOVINGWALL phase. That means that the level of adhesion can be different for every WALL or MOVINGWALL phase. The same applies to the

γ

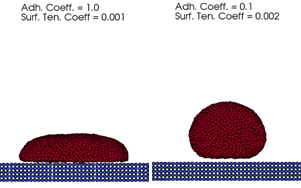
value for the surface tension forces. The balance between surface tension and adhesion forces can replicate qualitatively the physical contact angles between the fluid and the solid elements. An example of balancing adhesion and surface tension forces is shown in Figure 1.

The adhesion model can be used in conjunction with the more physical multiphase surface tension model. In that situation, the surface tension forces are physical and only the adhesion model is left to be tuned, which can be a significantly easier exercise.

Modeling Physical Behavior of Single Phase Surface Tension and Adhesion

The nanoFluidX team has performed a number of tests resulting in the development of consistent single phase surface tension and adhesion behavior. By consistency it is meant that if appropriate/desired behavior is found for a given resolution and a given surface tension or adhesion coefficient such behavior can be replicated for other resolutions by following the below methodology.

The simulation data show that the variations of surface tension coefficient $σ$ and adhesion coefficient $ϵ$ due to particle spacing $d x$ changes can be modeled as $α d x^{- β}$ . $α$ and $β$ are case dependent and will take different values depending on the resolution and specific phenomena of the simulation. It is recommended to set $β = 0.7$ and $0.95$ for surface tension and adhesion, respectively.

The procedure to obtain new

σ

or when

d x

changes is as follows:

Assume your current values are $d x_{c}$ , $σ_{c}$ , and $ϵ_{c}$ .
You have a new $d x_{n}$ and want to find $σ_{n}$ and $ϵ_{n}$ .
Set $β = 0.7$ for surface tension and use $β = 0.95$ for adhesion.
Use $d x_{c}$ and $σ_{c}$ or $ϵ_{c}$ and solve for $α$ .
For example:(3)
$α = \frac{σ_{c}}{d x_{c}^{0.7}}$
or (4)
$α = \frac{ϵ_{c}}{d x_{c}^{0.95}}$
Use the $α$ computed above to find $σ_{n}$ or $ϵ_{n}$ .
For example,(5)
$σ_{n} = α d x_{n}^{0.7}$
or (6)
$ϵ_{n} = α d x_{n}^{0.95}$

These approximations are to save time when you want to change $d x$ . They are not perfect fits and some iteration maybe needed to find the adequate values.